por favor me ajudem sei que a resposta e 3+2i
mais ja tirei a potencia e enpaquei , preciso resolver e apreender como se faz, tenho que levar terça feira para meu professor.
se nao entender minha questão pode ser outra com a mesma formula todos os i estao elevados a um numero.
Coloque em forma algébrica a+bi o numero complexo
i?-2i²+i??3i?
????????
i?? i?+i?


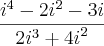

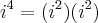




 (Note que é alterado o sinal da parte imaginária).
(Note que é alterado o sinal da parte imaginária).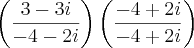


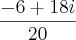
 --> Esse é o número complexo em forma algébrica após a divisão.
--> Esse é o número complexo em forma algébrica após a divisão.


