 por adauto martins » Seg Set 16, 2019 16:09
por adauto martins » Seg Set 16, 2019 16:09
(este-ita-escola tecnica do exercito,instituto tecnologico de aeronautica-exame de admissao 1947)
determinar os numeros complexos que gozam da propriedade de ter o quadrado e o complexo conjugado identicos.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por DanielFerreira » Ter Set 17, 2019 12:04
por DanielFerreira » Ter Set 17, 2019 12:04
adauto martins escreveu:(este-ita-escola tecnica do exercito,instituto tecnologico de aeronautica-exame de admissao 1947)
determinar os numeros complexos que gozam da propriedade de ter o quadrado e o complexo conjugado identicos.
Seja
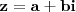
, com
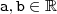
o
número complexo em questão. Portanto, ele deverá satisfazer
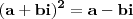
Segue,
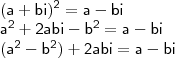
Comparando parte real e imaginária, teremos:
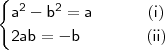
Resolvendo (ii),
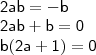 CASO I
CASO I:
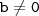
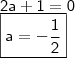
Substituindo em
(i),
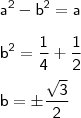
Logo,
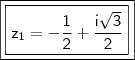
e
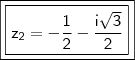 CASO II
CASO II:
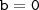
Substituindo em
(ii),
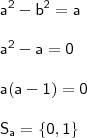
Logo,
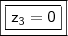
e
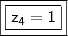
.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por adauto martins » Dom Set 22, 2019 12:01
por adauto martins » Dom Set 22, 2019 12:01
soluçao correta:
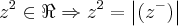
,pois
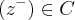
e onde
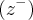
e o complexo conjudao de
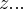
,logo:
![{z}^{2}=\sqrt[]{z.({z}^{-})}\Rightarrow {z}^{4}-z.({z}^{-})=0
z.({z}^{3}-({z}^{-})=0\Rightarrow z=0,{z}^{3}=({z}^{-})... {z}^{2}=\sqrt[]{z.({z}^{-})}\Rightarrow {z}^{4}-z.({z}^{-})=0
z.({z}^{3}-({z}^{-})=0\Rightarrow z=0,{z}^{3}=({z}^{-})...](/latexrender/pictures/311ae4a6903c1038e8d09e239fb90751.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Set 22, 2019 12:17
por adauto martins » Dom Set 22, 2019 12:17
correçao:
cometi um erro grave,pois
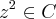
,pois
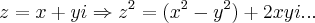
logo a soluçao do colega daniel e a soluçao correta...obrigado...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Out 11, 2019 10:34
por adauto martins » Sex Out 11, 2019 10:34
usando a soluçao anterior,faremos uma soluçao mais geral que a feita pelo colega daniel,que esta correta:
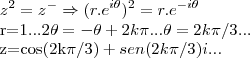
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:41
- 1 Respostas
- 12330 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:53
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:51
- 1 Respostas
- 12624 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:45
Polinômios
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:02
- 1 Respostas
- 4912 Exibições
- Última mensagem por adauto martins

Qui Set 19, 2019 09:39
Equações
-
- exerc.proposto
por adauto martins » Ter Set 17, 2019 10:30
- 1 Respostas
- 4211 Exibições
- Última mensagem por adauto martins

Seg Set 23, 2019 23:57
Equações
-
- exerc.proposto
por adauto martins » Ter Set 17, 2019 21:01
- 5 Respostas
- 4311 Exibições
- Última mensagem por adauto martins

Sex Out 04, 2019 14:05
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



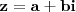 , com
, com 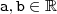 o número complexo em questão. Portanto, ele deverá satisfazer
o número complexo em questão. Portanto, ele deverá satisfazer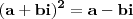
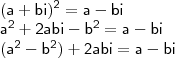
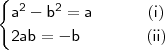
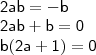
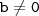
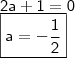
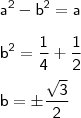
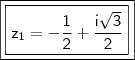 e
e 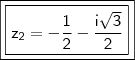
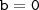
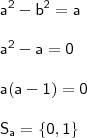
 e
e 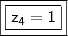 .
.
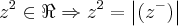 ,pois
,pois 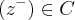 e onde
e onde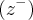 e o complexo conjudao de
e o complexo conjudao de 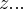 ,logo:
,logo:![{z}^{2}=\sqrt[]{z.({z}^{-})}\Rightarrow {z}^{4}-z.({z}^{-})=0
z.({z}^{3}-({z}^{-})=0\Rightarrow z=0,{z}^{3}=({z}^{-})... {z}^{2}=\sqrt[]{z.({z}^{-})}\Rightarrow {z}^{4}-z.({z}^{-})=0
z.({z}^{3}-({z}^{-})=0\Rightarrow z=0,{z}^{3}=({z}^{-})...](/latexrender/pictures/311ae4a6903c1038e8d09e239fb90751.png)

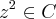 ,pois
,pois 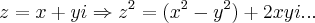

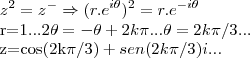



 , avisa que eu resolvo.
, avisa que eu resolvo.

