Bom dia,
Sou novo no forum e estou postando pela primeira vez para tirar as seguintes duvidas: Segue questões.
Dentro do disco D={z: |z-i|? 3/2}, no plano complexo, o número de pontos z=n+mi, onde i2=-1, com n e m sendo números inteiros, é:
(A) 4
(B) 5
(C) 8
(D) 9
No plano complexo, o subconjunto dos números definido por M = {z?C: |z +1| + |z ?1| = 4} representa
a) um segmento de reta.
b) uma hipérbole.
c) uma parábola.
d) uma elipse.
Não são questões muito difíceis, mas eu terminei o ensino médio tem algum tempo já e não consigo fazer e nos meus livros só aborda o básico sobre número complexo e não tem nenhum exemplo desse tipo, se puderem dar uma luz pra mim seria muito bom.


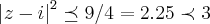 ...
...
 satisafaz as condiçoes...
satisafaz as condiçoes... q. nao tem raizes reais...logo nao podemos ter (0,m) q. satisfaz as condiçoes de soluçao...
q. nao tem raizes reais...logo nao podemos ter (0,m) q. satisfaz as condiçoes de soluçao...
 facilmente desenvolvemos
facilmente desenvolvemos 
 e centro em
e centro em  .
. temos
temos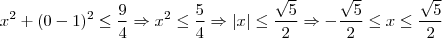
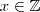 ,
,  ou
ou  .
. fazem par com estes três valores possíveis de
fazem par com estes três valores possíveis de 
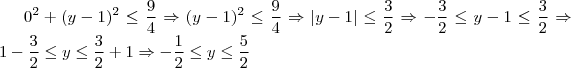
 ou
ou  .
.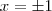 calculamos
calculamos 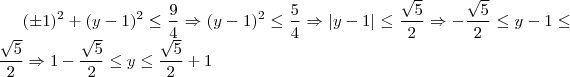
 tbem satisfaz a condiçao,entao as soluçoes sao...
tbem satisfaz a condiçao,entao as soluçoes sao...![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)