 por caroline1303 » Seg Out 08, 2012 01:15
por caroline1303 » Seg Out 08, 2012 01:15
Gente, preciso muito de ajuda em uma questão de complexos.
a questão é a seguinte:
Sendo o complexo w=
![\frac{\sqrt[2]{3}+i}{2} \frac{\sqrt[2]{3}+i}{2}](/latexrender/pictures/1f729916ff8c72eef107abce8a7ce29b.png)
e i =
![\sqrt[2]{-1} \sqrt[2]{-1}](/latexrender/pictures/836141fcbfaf783fc6b24244a217fad2.png)
(unidade imaginária)
a) determine a parte real e a parte imaginária dos complexos

e
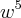
b) pode o complexo w ser raiz cúbica do complexo a= i?
c) Se w³ é uma das raízes quartas de um complexo z, determine todas as raízes restantes de z
-
caroline1303
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Out 08, 2012 00:58
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: farmácia
- Andamento: cursando
 por young_jedi » Seg Out 08, 2012 10:18
por young_jedi » Seg Out 08, 2012 10:18
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Parte real e imaginaria do n° complexo z e calculo
por Lee » Sáb Jun 19, 2010 23:05
- 1 Respostas
- 3044 Exibições
- Última mensagem por Anniinha

Seg Nov 01, 2010 20:58
Números Complexos
-
- unidade imaginaria (NUMEROS COMPLEXOS)
por lieberth » Qua Jun 10, 2009 20:51
- 6 Respostas
- 4874 Exibições
- Última mensagem por Molina

Sex Jun 12, 2009 20:18
Álgebra Elementar
-
- Ajuda para Limites Parte 2
por Optikool » Seg Jan 07, 2013 12:11
- 1 Respostas
- 1772 Exibições
- Última mensagem por e8group

Seg Jan 07, 2013 21:48
Cálculo: Limites, Derivadas e Integrais
-
- Questão de concurso- Parte/Todo
por Pri Ferreira » Qua Mar 21, 2012 14:01
- 1 Respostas
- 1780 Exibições
- Última mensagem por LuizAquino

Qua Mar 21, 2012 20:50
Álgebra Elementar
-
- Ajuda na equação do 1 grau (segunda parte)
por zekinha » Seg Jun 27, 2011 16:30
- 13 Respostas
- 7838 Exibições
- Última mensagem por zekinha

Ter Jun 28, 2011 12:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[2]{3}+i}{2} \frac{\sqrt[2]{3}+i}{2}](/latexrender/pictures/1f729916ff8c72eef107abce8a7ce29b.png) e i =
e i = ![\sqrt[2]{-1} \sqrt[2]{-1}](/latexrender/pictures/836141fcbfaf783fc6b24244a217fad2.png) (unidade imaginária)
(unidade imaginária) e
e 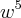


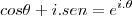
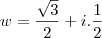
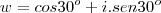
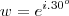
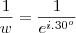
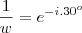
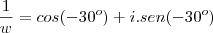
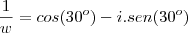
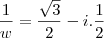


 .
.



