 por Danilo » Sex Ago 03, 2012 02:27
por Danilo » Sex Ago 03, 2012 02:27
Empacado em outro exercício... !
Qual o resultado da simplificação de:
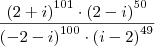
Bom, eu gostaria de resolver o exercício sem dividir cada expoente por 4, porque eu estou acompanhando o livro à risca e em teoria eu ainda não estudei esse método de dividir por 4.
A primeira coisa que tentei fazer foi, por exemplo, [(2+i)^2]^50

(2+i) e fui desenvolvendo. Fiz tanto no numerador quanto no denominador, mas não cheguei a uma solução. Agradeço a quem puder dar uma luz!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sex Ago 03, 2012 11:15
por e8group » Sex Ago 03, 2012 11:15
Bom dia ,
veja :

. Mas
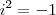
logo ,

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão - Números Complexos
por Glauber_Garcia » Qua Nov 28, 2012 21:25
- 2 Respostas
- 4778 Exibições
- Última mensagem por Direito

Qua Mar 13, 2013 01:15
Números Complexos
-
- [números complexos] questão unicentro
por Flavia R » Qui Ago 25, 2011 11:39
- 4 Respostas
- 3560 Exibições
- Última mensagem por Flavia R

Qui Ago 25, 2011 21:23
Números Complexos
-
- [Números complexos] Dúvida em questão
por iceman » Qui Mai 10, 2012 18:46
- 3 Respostas
- 2753 Exibições
- Última mensagem por fraol

Qui Mai 10, 2012 19:41
Números Complexos
-
- Números complexos - Questão chata
por iceman » Dom Mai 27, 2012 18:08
- 13 Respostas
- 7491 Exibições
- Última mensagem por DanielFerreira

Dom Mai 27, 2012 21:26
Números Complexos
-
- [Números Complexos] Questão envolvendo Potenciação
por everton_stark » Sáb Dez 26, 2015 22:49
- 1 Respostas
- 8730 Exibições
- Última mensagem por rzarour

Sex Abr 01, 2016 07:18
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
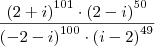
 (2+i) e fui desenvolvendo. Fiz tanto no numerador quanto no denominador, mas não cheguei a uma solução. Agradeço a quem puder dar uma luz!
(2+i) e fui desenvolvendo. Fiz tanto no numerador quanto no denominador, mas não cheguei a uma solução. Agradeço a quem puder dar uma luz!

 . Mas
. Mas 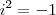 logo ,
logo ,
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.