Amanhã eu terei prova de calculo 3, e existem alguns exercicios da lista que não consegui chegar a um resultado, será que alguém pode me auxiliar a resolução?
1)resolver a equação
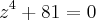 no conjunto dos números reais complexos e represente as soluções.
no conjunto dos números reais complexos e represente as soluções. Resposta:
![{z}_{0}=3\left(\frac{\sqrt[]{2}}{2} +i\frac{\sqrt[]{2}}{2}\right) {z}_{0}=3\left(\frac{\sqrt[]{2}}{2} +i\frac{\sqrt[]{2}}{2}\right)](/latexrender/pictures/503b5d617997dfefda442c594a30f787.png) e
e ![{z}_{1}=3\left(-\frac{\sqrt[]{2}}{2} -i\frac{\sqrt[]{2}}{2}\right) {z}_{1}=3\left(-\frac{\sqrt[]{2}}{2} -i\frac{\sqrt[]{2}}{2}\right)](/latexrender/pictures/e8f94a93811589f67e0dcefdbd73138d.png)
so que quando eu tentei resolver usando a formula das raizes eu consegui chegar em 4 respostas
2)Desenho o lugar geométrico dos afixos dos números complexos z tais que:
 considerar o (z) como Z barra ou (x-iy);
considerar o (z) como Z barra ou (x-iy);Sei que tenho que achar a equação e achar os pontos para traçar no plano de Argand-gauss, mas chego na equação:
 como devo simplificar para achar os pontos, ou dessa equação tiro os pontos e coloco no gráfico? essa seria uma equação de reta, separando o y e tirando a raíz do resto?
como devo simplificar para achar os pontos, ou dessa equação tiro os pontos e coloco no gráfico? essa seria uma equação de reta, separando o y e tirando a raíz do resto?Mas uma dúvida, em série de fourier, como achar a equação da reta paralela ao eixo x (negativo em x com os pontos
 e
e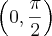 ) outra inclinada(com os pontos
) outra inclinada(com os pontos  e
e 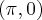 ), para iniciar os calculos?
), para iniciar os calculos?

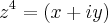 eu chego e duas equações e igualando parte real com real e imaginária com imaginária, eu consigo achar que x=y chegando assim nas duas respostas:
eu chego e duas equações e igualando parte real com real e imaginária com imaginária, eu consigo achar que x=y chegando assim nas duas respostas:![{z}_{0}=3(\frac{\sqrt[]{2}}{2}+i\frac{\sqrt[]{2}}{2}) {z}_{0}=3(\frac{\sqrt[]{2}}{2}+i\frac{\sqrt[]{2}}{2})](/latexrender/pictures/6b4ad10bb237f425bc202f1bc9e99732.png) e
e ![{z}_{1}=3(-\frac{\sqrt[]{2}}{2}-i\frac{\sqrt[]{2}}{2}) {z}_{1}=3(-\frac{\sqrt[]{2}}{2}-i\frac{\sqrt[]{2}}{2})](/latexrender/pictures/34006f2dcc3178f9259e73c13c753c30.png)
 e na segunda por matriz eu chego na equação
e na segunda por matriz eu chego na equação 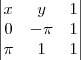


 , avisa que eu resolvo.
, avisa que eu resolvo.

