 por Colton » Qui Mai 12, 2011 12:29
por Colton » Qui Mai 12, 2011 12:29
+
+
Estou me debatendo com o seguinte exercício (que vou digitar sem símbolos):
(Exercício 303 de Fundamentos de Matemática Elementar vol. 5, 7ª edição, página 75.)
Determine o valor de A(n) = somatório de p=0 até n de (Cn,p)[2^(p)3^(n-p)-4^p], para todo n > 0.
Entendo que o somatório proposto é igual a 2^n.
Entendo que [2^(p)3^(n-p)-4^p]pode ser reescrito como (2/3)^p3^n-4^p
Mas não sei o que fazer com (2^n)[(2/3)^p3^n-4^p] para obter A(n) = 0, que é o gabarito.
Tem alguém aí para me dar uma ajudinha?
Sds
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por LuizAquino » Ter Mar 13, 2012 20:55
por LuizAquino » Ter Mar 13, 2012 20:55
Sei que essa dúvida é antiga (foi enviada no dia 12 de maio de 2011), mas segue a solução abaixo.
Colton escreveu:Estou me debatendo com o seguinte exercício (que vou digitar sem símbolos):
(Exercício 303 de Fundamentos de Matemática Elementar vol. 5, 7ª edição, página 75.)
Determine o valor de A(n) = somatório de p=0 até n de (Cn,p)[2^(p)3^(n-p)-4^p], para todo n > 0.
Entendo que o somatório proposto é igual a 2^n.
Entendo que [2^(p)3^(n-p)-4^p]pode ser reescrito como (2/3)^p3^n-4^p
Mas não sei o que fazer com (2^n)[(2/3)^p3^n-4^p] para obter A(n) = 0, que é o gabarito.
Primeiro, vamos escrever o exercício usando a notação adequada:
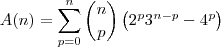
Agora, note que:
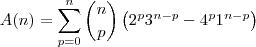
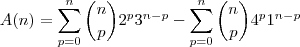
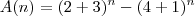
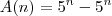
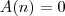
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


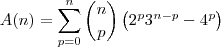
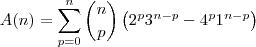
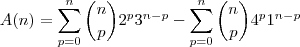
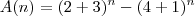
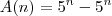
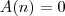



 , avisa que eu resolvo.
, avisa que eu resolvo.

