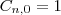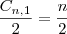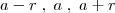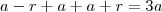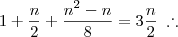por Jonatan » Qua Jun 16, 2010 18:12
por Jonatan » Qua Jun 16, 2010 18:12
Os três primeiros coeficientes do desenvolvimento de
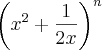
segundo as potências decrescentes de x estão em PA. O valor de n é um número:
a) primo
b) quadrado perfeito
c) cubo perfeito
d) maior que 9 e menor que 15
Gabarito: c) cubo perfeito.
Alguém poderia resolver essa questão pra mim? Não faço ideia de como desenvolver sem saber o valor do expoente n... Desde já agradeço.
-
Jonatan
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Jun 16, 2010 13:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Douglasm » Qua Jun 16, 2010 21:34
por Douglasm » Qua Jun 16, 2010 21:34
Olá Jonatan. Comecemos lembrando do desenvolvimento binomial (prestando muita atenção ao 1/2x) e estabelecendo os coeficientes:
1º -
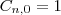
2º -
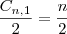
3º -

Note que as divisões por 2 e por 8 se deram por termos elevado 1/2x a primeira e segunda potência, respectivamente.
Como esta é uma P.A., os coeficientes se encontram na seguinte forma:
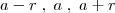
Em que
a representa
n/2 e
r a razão da progressão.
É evidente que:
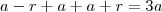
Do mesmo modo:
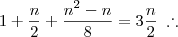


Encontrando as raízes dessa equação, vemos que
n = 8 (haja vista que o resultado n=1 não satisfaz as condições do problema). Continuando, concluímos que
n é um cubo perfeito.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
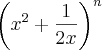 segundo as potências decrescentes de x estão em PA. O valor de n é um número:
segundo as potências decrescentes de x estão em PA. O valor de n é um número: