-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478174 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531852 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495378 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 705813 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2121766 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Humberto Batista » Ter Out 28, 2014 09:32
por Humberto Batista » Ter Out 28, 2014 09:32
Bom dia!
Estudo pra concurso em minha casa e após ter resolvido diversas questões triviais de Binômio de Newton com aplicação de formula, me deparei com essa questão aonde não consegui evoluir na sua resolução.
Sejam a e b dois números reais quaisquer e p um número primo. Raramente é verdade que

Em alguns casos a igualdade ocorre, quais casos são esses?
Desde já agradeço a atenção de todos.
-
Humberto Batista
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 27, 2014 22:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por e8group » Ter Out 28, 2014 12:32
por e8group » Ter Out 28, 2014 12:32
Perceba que se pelo menos um dos números reais a,b for nulo , é claro que a =dade é verificada .Agora suponha ambos não nulos . Se p é primo , e temos

certamente

é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial
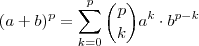
que pode ser escrito como
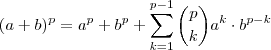
.Devemos então estudar quando ,
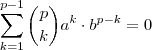
para a,b não nulos que equivale estudar a igualdade abaixo
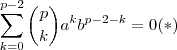
.(basta dividir ambos lados por ab) .
Agora a cada fixado não nulo façamos corresponder um polinômio de grau p-2 dado por ,

.
Afirmação : O polinômio acima possui ao menos uma raíz real . (exercício )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Humberto Batista » Ter Out 28, 2014 13:51
por Humberto Batista » Ter Out 28, 2014 13:51
Olá santiago, obrigado pela resposta.
Vá por favor vá desculpando a minha ignorância, estou retomando aos estudos e matemática não é o meu forte, tenho dificuldades de entender. Quer dizer que a igualdade só ocorre quando "a" ou "b" for nulo?
santhiago escreveu:Perceba que se pelo menos um dos números reais a,b for nulo , é claro que a =dade é verificada .Agora suponha ambos não nulos . Se p é primo , e temos

certamente

é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial
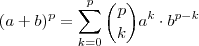
que pode ser escrito como
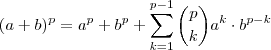
.Devemos então estudar quando ,
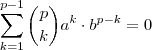
para a,b não nulos que equivale estudar a igualdade abaixo
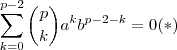
.(basta dividir ambos lados por ab) .
Agora a cada fixado não nulo façamos corresponder um polinômio de grau p-2 dado por ,

.
Afirmação : O polinômio acima possui ao menos uma raíz real . (exercício )
-
Humberto Batista
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 27, 2014 22:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por e8group » Ter Out 28, 2014 15:48
por e8group » Ter Out 28, 2014 15:48
Humberto Batista escreveu:Olá santiago, obrigado pela resposta.
Vá por favor vá desculpando a minha ignorância, estou retomando aos estudos e matemática não é o meu forte, tenho dificuldades de entender. Quer dizer que a igualdade só ocorre quando "a" ou "b" for nulo?
Olá ! Não necessariamente , podemos ter pares de números nao nulos os quais satisfazem a equação . Tome a = 3 e b = -3 .De forma geral fixado qualquer b , pondo a = -b tem-se a igualdade para qualquer p primo maior q 2(na verdade p/ qq impar tbm vale ) .Evidentemente temos mais soluções que estas ,explicitar a forma geral das soluções talvez não seja simples , entretanto podemos provar a existência de tal soluções .Todo polinômio de grau impar possui pelo menos uma raiz real ( isso pq estes a imagem destes polinômios oscilam o sinal para valores arbitrariamente grandes ( negativamente e positivamente ) do seu domínio e são funções continuas , daí o teorema do valor intermediário assegura a existência da raiz real , mas não sei se vc está familiarizado com estes conceitos ) .Embora deparamos com a infinitude de pares (a,b) que satisfazem a eq. , há mais pares de números reais que não satisfazem a igualdade do q se possa imaginar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Ter Out 28, 2014 23:50
por Russman » Ter Out 28, 2014 23:50
Achei a questão interessante e , portanto, gostaria de fazer alguns comentários.
De fato, podemos escrever

Aqui fixamos o valor de

e buscamos valores de

tal que

. Evidentemente,

é solução. Note que

Também,

é solução para

. Note que
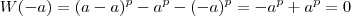
já que se p é primo(e portanto ímpar)

.
Disto, notamos que
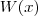
é sempre divisível por
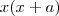
. Assim, reescrevemos
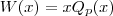
, onde

. [O subíndice p é para mostrar que para cada p existe um polinômio diferente.]
No que o grau de

é
![g[Q(x)] = p-2 g[Q(x)] = p-2](/latexrender/pictures/d439b3e0b9bf6be79416b41d356bebf7.png)
. Como

é primo e todo primo(a exceção de 2) é ímpar o número
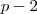
é ímpar também. Assim, o grau de

é ímpar e o teorema das raízes assegura que existe ao menos uma raíz real para este. Claro, esta raíz é

como já verificamos anteriormente. De fato, podemos escrever

onde

é o resultado da divisão de

por

.
Outro fato interessante é que
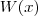
é sempre divisível por

, para p ímpar. Acredito que não seja muito dificil de mostrar isso.
Além disso( o que é um pouco mais difícil) é mostrar que
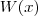
é também sempre divisível por

.
De fato,
![W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ] W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ]](/latexrender/pictures/45e319deeaba9d8f25fe679f742bd249.png)
que é nulo toda vez que
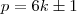
, com

. Mas, esta expressão captura todos os números

divisíveis por 6 e , portanto(quase certeza que), todos os primos. Daí,
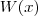
é sempre divisível por

. Assim, podemos escrever

O problema então se resume a relacionar

com

e estabelecer as condições de existência de raízes reais para o polinômio
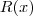
. Eu acredito que as mesmas não existam.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Binômio de Newton
por Giordane Junior » Sex Dez 03, 2010 00:46
- 0 Respostas
- 7744 Exibições
- Última mensagem por Giordane Junior

Sex Dez 03, 2010 00:46
Binômio de Newton
-
- (PUC-PR)BINOMIO DE NEWTON
por natanskt » Seg Dez 06, 2010 10:54
- 1 Respostas
- 6926 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 11:54
Binômio de Newton
-
- Binômio de Newton
por natanskt » Seg Dez 06, 2010 12:07
- 1 Respostas
- 8309 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:07
Binômio de Newton
-
- Binomio de Newton.
por 380625 » Sex Mar 11, 2011 12:57
- 1 Respostas
- 2617 Exibições
- Última mensagem por MarceloFantini

Sex Mar 11, 2011 16:20
Binômio de Newton
-
- Binomio de newton
 por Fabricio dalla » Sex Abr 01, 2011 01:13
por Fabricio dalla » Sex Abr 01, 2011 01:13
- 8 Respostas
- 7529 Exibições
- Última mensagem por LuizAquino

Sáb Jul 23, 2011 19:12
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Em alguns casos a igualdade ocorre, quais casos são esses?
Em alguns casos a igualdade ocorre, quais casos são esses?

 certamente
certamente  é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial
é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial 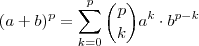 que pode ser escrito como
que pode ser escrito como 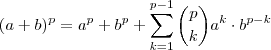 .Devemos então estudar quando ,
.Devemos então estudar quando , 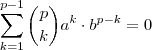 para a,b não nulos que equivale estudar a igualdade abaixo
para a,b não nulos que equivale estudar a igualdade abaixo 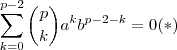 .(basta dividir ambos lados por ab) .
.(basta dividir ambos lados por ab) . .
.

 e buscamos valores de
e buscamos valores de  tal que
tal que  . Evidentemente,
. Evidentemente,  é solução. Note que
é solução. Note que
 é solução para
é solução para  . Note que
. Note que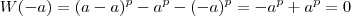
 .
.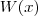 é sempre divisível por
é sempre divisível por 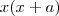 . Assim, reescrevemos
. Assim, reescrevemos 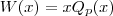 , onde
, onde . [O subíndice p é para mostrar que para cada p existe um polinômio diferente.]
. [O subíndice p é para mostrar que para cada p existe um polinômio diferente.] é
é ![g[Q(x)] = p-2 g[Q(x)] = p-2](/latexrender/pictures/d439b3e0b9bf6be79416b41d356bebf7.png) . Como
. Como 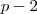 é ímpar também. Assim, o grau de
é ímpar também. Assim, o grau de 
 é o resultado da divisão de
é o resultado da divisão de  por
por  .
. , para p ímpar. Acredito que não seja muito dificil de mostrar isso.
, para p ímpar. Acredito que não seja muito dificil de mostrar isso.  .
.![W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ] W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ]](/latexrender/pictures/45e319deeaba9d8f25fe679f742bd249.png)
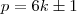 , com
, com  . Mas, esta expressão captura todos os números
. Mas, esta expressão captura todos os números  divisíveis por 6 e , portanto(quase certeza que), todos os primos. Daí,
divisíveis por 6 e , portanto(quase certeza que), todos os primos. Daí, 
 com
com 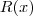 . Eu acredito que as mesmas não existam.
. Eu acredito que as mesmas não existam. } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: