 por cristina » Dom Ago 22, 2010 13:45
por cristina » Dom Ago 22, 2010 13:45
1 - No desenvolvimento do binomio
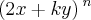
, segundo potencias decrescentes de x, o terceiro termo é 80
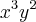
, n pertence N e k > o. Então o valor n + k é:
2- sejam 2 retas paralelas r e s, tomando-se 5 pontos em r e 6 pontos em s, quantas retas esses 11 pontos determinam?
Se alguem puder me ajudar agradeço.
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por VtinxD » Dom Ago 22, 2010 14:13
por VtinxD » Dom Ago 22, 2010 14:13
1°Problema-
Em problemas deste tipo é bom usar o termo geral de um binomio.
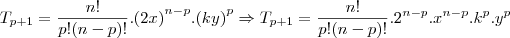
Logo:

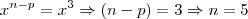
Agora só falta achar o valor de k ,e como já possuimos o valor de n e p teremos só que analisar o resto da equação:

[tex]k + n = 5 + \frac{1}{2} \Rightarrow k + n = \frac{11}{2}
Espero ter ajudado e que esteja certo

.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por cristina » Qui Ago 26, 2010 11:42
por cristina » Qui Ago 26, 2010 11:42
Olá
As possiveis alternativas são:
a) 6
b) 5
c) 8
d) 9
e) 7
nesse caso não consegui entender, o que esta errado.
abs
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Douglasm » Qui Ago 26, 2010 13:20
por Douglasm » Qui Ago 26, 2010 13:20
Na verdade foi só uma falta de atenção ao finalizar o problema. VtinxD fez:

O erro foi só elevar dois a quinta, quando na verdade ele deveria ser elevado ao cubo. Logo:

Isso faz com que a resposta seja letra "a", 6.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Binomio
por carmem » Sex Jun 19, 2009 21:21
- 3 Respostas
- 2029 Exibições
- Última mensagem por Molina

Sex Jun 19, 2009 23:08
Binômio de Newton
-
- Binômio
por thadeu » Qua Nov 18, 2009 13:00
- 1 Respostas
- 1367 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 13:35
Binômio de Newton
-
- Binômio de Newton
por Giordane Junior » Sex Dez 03, 2010 00:46
- 0 Respostas
- 8108 Exibições
- Última mensagem por Giordane Junior

Sex Dez 03, 2010 00:46
Binômio de Newton
-
- (PUC-PR)BINOMIO DE NEWTON
por natanskt » Seg Dez 06, 2010 10:54
- 1 Respostas
- 7390 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 11:54
Binômio de Newton
-
- Binômio de Newton
por natanskt » Seg Dez 06, 2010 12:07
- 1 Respostas
- 8817 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:07
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
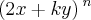 , segundo potencias decrescentes de x, o terceiro termo é 80
, segundo potencias decrescentes de x, o terceiro termo é 80 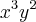 , n pertence N e k > o. Então o valor n + k é:
, n pertence N e k > o. Então o valor n + k é:

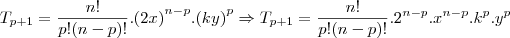

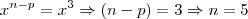

 .
.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.