 por Humberto Batista » Ter Out 28, 2014 09:32
por Humberto Batista » Ter Out 28, 2014 09:32
Bom dia!
Estudo pra concurso em minha casa e após ter resolvido diversas questões triviais de Binômio de Newton com aplicação de formula, me deparei com essa questão aonde não consegui evoluir na sua resolução.
Sejam a e b dois números reais quaisquer e p um número primo. Raramente é verdade que

Em alguns casos a igualdade ocorre, quais casos são esses?
Desde já agradeço a atenção de todos.
-
Humberto Batista
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 27, 2014 22:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por e8group » Ter Out 28, 2014 12:32
por e8group » Ter Out 28, 2014 12:32
Perceba que se pelo menos um dos números reais a,b for nulo , é claro que a =dade é verificada .Agora suponha ambos não nulos . Se p é primo , e temos

certamente

é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial
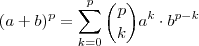
que pode ser escrito como
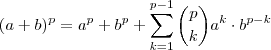
.Devemos então estudar quando ,
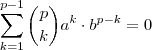
para a,b não nulos que equivale estudar a igualdade abaixo
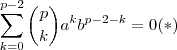
.(basta dividir ambos lados por ab) .
Agora a cada fixado não nulo façamos corresponder um polinômio de grau p-2 dado por ,

.
Afirmação : O polinômio acima possui ao menos uma raíz real . (exercício )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Humberto Batista » Ter Out 28, 2014 13:51
por Humberto Batista » Ter Out 28, 2014 13:51
Olá santiago, obrigado pela resposta.
Vá por favor vá desculpando a minha ignorância, estou retomando aos estudos e matemática não é o meu forte, tenho dificuldades de entender. Quer dizer que a igualdade só ocorre quando "a" ou "b" for nulo?
santhiago escreveu:Perceba que se pelo menos um dos números reais a,b for nulo , é claro que a =dade é verificada .Agora suponha ambos não nulos . Se p é primo , e temos

certamente

é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial
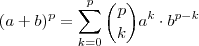
que pode ser escrito como
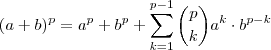
.Devemos então estudar quando ,
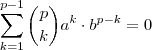
para a,b não nulos que equivale estudar a igualdade abaixo
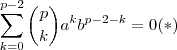
.(basta dividir ambos lados por ab) .
Agora a cada fixado não nulo façamos corresponder um polinômio de grau p-2 dado por ,

.
Afirmação : O polinômio acima possui ao menos uma raíz real . (exercício )
-
Humberto Batista
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 27, 2014 22:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por e8group » Ter Out 28, 2014 15:48
por e8group » Ter Out 28, 2014 15:48
Humberto Batista escreveu:Olá santiago, obrigado pela resposta.
Vá por favor vá desculpando a minha ignorância, estou retomando aos estudos e matemática não é o meu forte, tenho dificuldades de entender. Quer dizer que a igualdade só ocorre quando "a" ou "b" for nulo?
Olá ! Não necessariamente , podemos ter pares de números nao nulos os quais satisfazem a equação . Tome a = 3 e b = -3 .De forma geral fixado qualquer b , pondo a = -b tem-se a igualdade para qualquer p primo maior q 2(na verdade p/ qq impar tbm vale ) .Evidentemente temos mais soluções que estas ,explicitar a forma geral das soluções talvez não seja simples , entretanto podemos provar a existência de tal soluções .Todo polinômio de grau impar possui pelo menos uma raiz real ( isso pq estes a imagem destes polinômios oscilam o sinal para valores arbitrariamente grandes ( negativamente e positivamente ) do seu domínio e são funções continuas , daí o teorema do valor intermediário assegura a existência da raiz real , mas não sei se vc está familiarizado com estes conceitos ) .Embora deparamos com a infinitude de pares (a,b) que satisfazem a eq. , há mais pares de números reais que não satisfazem a igualdade do q se possa imaginar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Ter Out 28, 2014 23:50
por Russman » Ter Out 28, 2014 23:50
Achei a questão interessante e , portanto, gostaria de fazer alguns comentários.
De fato, podemos escrever

Aqui fixamos o valor de

e buscamos valores de

tal que

. Evidentemente,

é solução. Note que

Também,

é solução para

. Note que
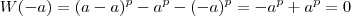
já que se p é primo(e portanto ímpar)

.
Disto, notamos que
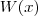
é sempre divisível por
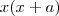
. Assim, reescrevemos
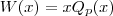
, onde

. [O subíndice p é para mostrar que para cada p existe um polinômio diferente.]
No que o grau de

é
![g[Q(x)] = p-2 g[Q(x)] = p-2](/latexrender/pictures/d439b3e0b9bf6be79416b41d356bebf7.png)
. Como

é primo e todo primo(a exceção de 2) é ímpar o número
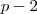
é ímpar também. Assim, o grau de

é ímpar e o teorema das raízes assegura que existe ao menos uma raíz real para este. Claro, esta raíz é

como já verificamos anteriormente. De fato, podemos escrever

onde

é o resultado da divisão de

por

.
Outro fato interessante é que
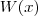
é sempre divisível por

, para p ímpar. Acredito que não seja muito dificil de mostrar isso.
Além disso( o que é um pouco mais difícil) é mostrar que
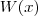
é também sempre divisível por

.
De fato,
![W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ] W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ]](/latexrender/pictures/45e319deeaba9d8f25fe679f742bd249.png)
que é nulo toda vez que
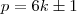
, com

. Mas, esta expressão captura todos os números

divisíveis por 6 e , portanto(quase certeza que), todos os primos. Daí,
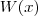
é sempre divisível por

. Assim, podemos escrever

O problema então se resume a relacionar

com

e estabelecer as condições de existência de raízes reais para o polinômio
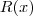
. Eu acredito que as mesmas não existam.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Binômio de Newton
por Giordane Junior » Sex Dez 03, 2010 00:46
- 0 Respostas
- 8105 Exibições
- Última mensagem por Giordane Junior

Sex Dez 03, 2010 00:46
Binômio de Newton
-
- (PUC-PR)BINOMIO DE NEWTON
por natanskt » Seg Dez 06, 2010 10:54
- 1 Respostas
- 7387 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 11:54
Binômio de Newton
-
- Binômio de Newton
por natanskt » Seg Dez 06, 2010 12:07
- 1 Respostas
- 8812 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:07
Binômio de Newton
-
- Binomio de Newton.
por 380625 » Sex Mar 11, 2011 12:57
- 1 Respostas
- 3021 Exibições
- Última mensagem por MarceloFantini

Sex Mar 11, 2011 16:20
Binômio de Newton
-
- Binomio de newton
 por Fabricio dalla » Sex Abr 01, 2011 01:13
por Fabricio dalla » Sex Abr 01, 2011 01:13
- 8 Respostas
- 8425 Exibições
- Última mensagem por LuizAquino

Sáb Jul 23, 2011 19:12
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Em alguns casos a igualdade ocorre, quais casos são esses?
Em alguns casos a igualdade ocorre, quais casos são esses?

 certamente
certamente  é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial
é impar (basta verificar que o caso p = 2 ) . Pro caso mais geral , temos graças ao teor. Binomial 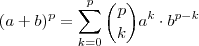 que pode ser escrito como
que pode ser escrito como 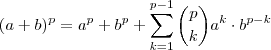 .Devemos então estudar quando ,
.Devemos então estudar quando , 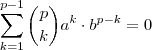 para a,b não nulos que equivale estudar a igualdade abaixo
para a,b não nulos que equivale estudar a igualdade abaixo 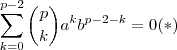 .(basta dividir ambos lados por ab) .
.(basta dividir ambos lados por ab) . .
.

 e buscamos valores de
e buscamos valores de  tal que
tal que  . Evidentemente,
. Evidentemente,  é solução. Note que
é solução. Note que
 é solução para
é solução para  . Note que
. Note que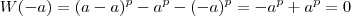
 .
.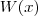 é sempre divisível por
é sempre divisível por 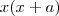 . Assim, reescrevemos
. Assim, reescrevemos 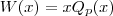 , onde
, onde . [O subíndice p é para mostrar que para cada p existe um polinômio diferente.]
. [O subíndice p é para mostrar que para cada p existe um polinômio diferente.] é
é ![g[Q(x)] = p-2 g[Q(x)] = p-2](/latexrender/pictures/d439b3e0b9bf6be79416b41d356bebf7.png) . Como
. Como 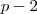 é ímpar também. Assim, o grau de
é ímpar também. Assim, o grau de 
 é o resultado da divisão de
é o resultado da divisão de  por
por  .
. , para p ímpar. Acredito que não seja muito dificil de mostrar isso.
, para p ímpar. Acredito que não seja muito dificil de mostrar isso.  .
.![W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ] W\left ( -\frac{a}{2}(1 \pm i\sqrt{3}) \right ) = a^p \left [ 2\cos(p\frac{\pi}{3})-1 \right ]](/latexrender/pictures/45e319deeaba9d8f25fe679f742bd249.png)
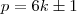 , com
, com  . Mas, esta expressão captura todos os números
. Mas, esta expressão captura todos os números  divisíveis por 6 e , portanto(quase certeza que), todos os primos. Daí,
divisíveis por 6 e , portanto(quase certeza que), todos os primos. Daí, 
 com
com 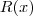 . Eu acredito que as mesmas não existam.
. Eu acredito que as mesmas não existam.