![({\frac{\sqrt[2]{3}\sqrt[6]{x}}{\sqrt[2]{5x}}-\frac{\sqrt[3]{5x}}{\sqrt[3]{3}\sqrt[6]{x}}})^{12} ({\frac{\sqrt[2]{3}\sqrt[6]{x}}{\sqrt[2]{5x}}-\frac{\sqrt[3]{5x}}{\sqrt[3]{3}\sqrt[6]{x}}})^{12}](/latexrender/pictures/fada54dc420f83d9a108cfe0679b647a.png)
olha eu perguntei pro meu professor ele falou q tinha q resolve os radicais dentro do binomio. bom entao o que entendi dele seria resolver essa moleza :( ate onde der para poder identificar os o coeficiente a e o X" para jogar na formula. o problema racionalizaçao so serve pra indice 2 que eu me lembre.Então acredito que se deve chegar de outro modo aos coeficientes. se possivel me oriente o que devo fazer!!.
obs(será que o coeficiente de X" ai seria o x de maior expoente no caso x elevado a 2/3 ?)
resposta:
![165\sqrt[3]{75} 165\sqrt[3]{75}](/latexrender/pictures/6becbc7c377927576ddabf23d26ae909.png)
desde ja agradeço



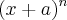 sempre o coeficiente "a" para se jogar na formula de termo geral, vai ser o segundo elemento
sempre o coeficiente "a" para se jogar na formula de termo geral, vai ser o segundo elemento 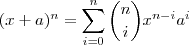
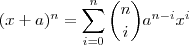
 , é:
, é:
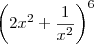 ?
?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)