Os mestres me amparem se eu estiver falando uma atrocidade... mas, vamos por parte...
Vamos analisar bem a situação...
Cada termo será definido pelo produto de um coeficiente por uma potência de cada termo, correto...
Note que o primeiro termo é a/x...
e o segundo raíz de x
Vejamos uma coisa... em cada termo, a raíz dividirá pela metade o expoente do segundo termo... e, como resultado do produto, o expoente do x do denominador do primeiro termo será subtraído do expoente segundo termo, que estará no numerador... correto?
Sabemos que um binomio elevado a n terá n+1 termos, correto? Este, então, terá 13 termos... sendo t a posição de cada termo no resultado, o expoente do primeiro termo do binômio é (n+1)-t e do segundo termo é t-1... tudo certo até agora?
Então, chamando o coeficiente do termo t de
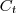
teremos:
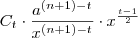
Esse termo resultará em:
![C_t \cdot a \cdot x^{\frac{t-1}{2}-[(n+1)-t]} C_t \cdot a \cdot x^{\frac{t-1}{2}-[(n+1)-t]}](/latexrender/pictures/5d3f89a177ace73b162b7378924d2a09.png)
Como o que nos importa, no primeiro momento, é o expoente de x, que é 5:
![\\
\frac{t-1}{2}-[(n+1)-t] = 5\\
\frac{t-1}{2}-[(12+1)-t] = 5\\
\frac{t-1}{2}-[13-t]=5\\
\frac{t-1}{2}-13+t=5\\
\frac{t}{2}+t-13-\frac{1}{2}=5\\
\frac{t+2t}{2}=5+13+\frac{1}{2}\\
\frac{3t}{2}=\frac{10+26+1}{2}\\
3t = 37\\
t = 37/3 \\
\frac{t-1}{2}-[(n+1)-t] = 5\\
\frac{t-1}{2}-[(12+1)-t] = 5\\
\frac{t-1}{2}-[13-t]=5\\
\frac{t-1}{2}-13+t=5\\
\frac{t}{2}+t-13-\frac{1}{2}=5\\
\frac{t+2t}{2}=5+13+\frac{1}{2}\\
\frac{3t}{2}=\frac{10+26+1}{2}\\
3t = 37\\
t = 37/3](/latexrender/pictures/b73f0b25e91a429209e0318fb4b950be.png)
Como não existe tal termo, logo, não haverá, a rigor, um termo com x elevado a 5...
Para concluir o raciocínio... podemos desenvolver o binomio e veremos que os coeficientes serão:
1;12;66;220;495;792;792;792;495;220;66;12;1
cada um multiplicando
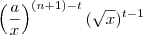
Então teremos
![\\
1\left[ \left (\frac{a}{x}\right )^{12}(\sqrt x)^0\right ] +
12\left[\left(\frac{a}{x} \right )^{11} (\sqrt x)^1 \right ] +
66 \left[\left(\frac{a}{x} \right )^{10} (\sqrt x)^2 \right ] +
220 \left[\left(\frac{a}{x} \right )^{9} (\sqrt x)^3 \right ] +
495 \left[\left(\frac{a}{x} \right )^{8} (\sqrt x)^4 \right ] +
792 \left[\left(\frac{a}{x} \right )^{7} (\sqrt x)^5 \right ] +
792 \left[\left(\frac{a}{x} \right )^{6} (\sqrt x)^6 \right ] +
792 \left[\left(\frac{a}{x} \right )^{5} (\sqrt x)^7 \right ] +
495 \left[\left(\frac{a}{x} \right )^{4} (\sqrt x)^8 \right ] +
220 \left[\left(\frac{a}{x} \right )^{3} (\sqrt x)^9 \right ] +
66 \left[\left(\frac{a}{x} \right )^{2} (\sqrt x)^{10} \right ] +
12 \left[\left(\frac{a}{x} \right )^{1} (\sqrt x)^{11} \right ] +
1 \left[\left(\frac{a}{x} \right )^{0} (\sqrt x)^{12} \right ] \\
1\left[ \left (\frac{a}{x}\right )^{12}(\sqrt x)^0\right ] +
12\left[\left(\frac{a}{x} \right )^{11} (\sqrt x)^1 \right ] +
66 \left[\left(\frac{a}{x} \right )^{10} (\sqrt x)^2 \right ] +
220 \left[\left(\frac{a}{x} \right )^{9} (\sqrt x)^3 \right ] +
495 \left[\left(\frac{a}{x} \right )^{8} (\sqrt x)^4 \right ] +
792 \left[\left(\frac{a}{x} \right )^{7} (\sqrt x)^5 \right ] +
792 \left[\left(\frac{a}{x} \right )^{6} (\sqrt x)^6 \right ] +
792 \left[\left(\frac{a}{x} \right )^{5} (\sqrt x)^7 \right ] +
495 \left[\left(\frac{a}{x} \right )^{4} (\sqrt x)^8 \right ] +
220 \left[\left(\frac{a}{x} \right )^{3} (\sqrt x)^9 \right ] +
66 \left[\left(\frac{a}{x} \right )^{2} (\sqrt x)^{10} \right ] +
12 \left[\left(\frac{a}{x} \right )^{1} (\sqrt x)^{11} \right ] +
1 \left[\left(\frac{a}{x} \right )^{0} (\sqrt x)^{12} \right ]](/latexrender/pictures/6869473ae78dd41f40f3582da1a09e88.png)
Que resultará, ainda, em:
![\\
1\left[\frac{a^{12}\sqrt x ^{0}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x ^{1}}{x^{11}} \right ] +
66\left[\frac{a^{10}\sqrt x ^{2}}{x^{10}} \right ] +
220\left[\frac{a^{9}\sqrt x ^{3}}{x^{9}} \right ] +
495\left[\frac{a^{8}\sqrt x ^{4}}{x^{8}} \right ] +
792\left[\frac{a^{7}\sqrt x ^{5}}{x^{7}} \right ] +
792\left[\frac{a^{6}\sqrt x ^{6}}{x^{6}} \right ] +
792\left[\frac{a^{5}\sqrt x ^{7}}{x^{5}} \right ] +
495\left[\frac{a^{4}\sqrt x ^{8}}{x^{4}} \right ] +
220\left[\frac{a^{3}\sqrt x ^{9}}{x^{3}} \right ] +
66\left[\frac{a^{2}\sqrt x ^{10}}{x^{2}} \right ] +
12\left[\frac{a^{1}\sqrt x ^{11}}{x^{1}} \right ] +
1\left[\frac{a^{0}\sqrt x ^{12}}{x^{0}} \right ] \\
1\left[\frac{a^{12}\sqrt x ^{0}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x ^{1}}{x^{11}} \right ] +
66\left[\frac{a^{10}\sqrt x ^{2}}{x^{10}} \right ] +
220\left[\frac{a^{9}\sqrt x ^{3}}{x^{9}} \right ] +
495\left[\frac{a^{8}\sqrt x ^{4}}{x^{8}} \right ] +
792\left[\frac{a^{7}\sqrt x ^{5}}{x^{7}} \right ] +
792\left[\frac{a^{6}\sqrt x ^{6}}{x^{6}} \right ] +
792\left[\frac{a^{5}\sqrt x ^{7}}{x^{5}} \right ] +
495\left[\frac{a^{4}\sqrt x ^{8}}{x^{4}} \right ] +
220\left[\frac{a^{3}\sqrt x ^{9}}{x^{3}} \right ] +
66\left[\frac{a^{2}\sqrt x ^{10}}{x^{2}} \right ] +
12\left[\frac{a^{1}\sqrt x ^{11}}{x^{1}} \right ] +
1\left[\frac{a^{0}\sqrt x ^{12}}{x^{0}} \right ]](/latexrender/pictures/510bba62d9ecff8acca314885a6762dd.png)
Vamos simplificar as raízes:
![\\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}x}{x^{10}} \right ] +
220\left[\frac{a^{9}x\sqrt x}{x^{9}} \right ] +
495\left[\frac{a^{8}x ^{2}}{x^{8}} \right ] +
792\left[\frac{a^{7}x^2\sqrt x}{x^{7}} \right ] +
792\left[\frac{a^{6}x ^{3}}{x^{6}} \right ] +
792\left[\frac{a^{5}x ^{3}\sqrt x}{x^{5}} \right ] +
495\left[\frac{a^{4}x ^{4}}{x^{4}} \right ] +
220\left[\frac{a^{3}x ^{4}\sqrt x}{x^{3}} \right ] +
66\left[\frac{a^{2}x ^{5}}{x^{2}} \right ] +
12\left[\frac{ax ^{5}\sqrt x}{x^{1}} \right ] +
1\left[x ^{6}] \\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}x}{x^{10}} \right ] +
220\left[\frac{a^{9}x\sqrt x}{x^{9}} \right ] +
495\left[\frac{a^{8}x ^{2}}{x^{8}} \right ] +
792\left[\frac{a^{7}x^2\sqrt x}{x^{7}} \right ] +
792\left[\frac{a^{6}x ^{3}}{x^{6}} \right ] +
792\left[\frac{a^{5}x ^{3}\sqrt x}{x^{5}} \right ] +
495\left[\frac{a^{4}x ^{4}}{x^{4}} \right ] +
220\left[\frac{a^{3}x ^{4}\sqrt x}{x^{3}} \right ] +
66\left[\frac{a^{2}x ^{5}}{x^{2}} \right ] +
12\left[\frac{ax ^{5}\sqrt x}{x^{1}} \right ] +
1\left[x ^{6}]](/latexrender/pictures/00481cca490c4695528e654e7a4c34dd.png)
E, agora, operar a divisão de x por x:
![\\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}}{x^{9}} \right ] +
220\left[\frac{a^{9}\sqrt x}{x^{8}} \right ] +
495\left[\frac{a^{8}}{x^{6}} \right ] +
792\left[\frac{a^{7}\sqrt x}{x^{5}} \right ] +
792\left[\frac{a^{6}}{x^{3}} \right ] +
792\left[\frac{a^{5}\sqrt x}{x^{2}} \right ] +
495\left[a^{4}\right ] +
220\left[a^{3}x\right ] +
66\left[a^{2}x ^{3}\right ] +
12\left[ax ^{4}\sqrt x \right ] +
1\left[x ^{6}] \\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}}{x^{9}} \right ] +
220\left[\frac{a^{9}\sqrt x}{x^{8}} \right ] +
495\left[\frac{a^{8}}{x^{6}} \right ] +
792\left[\frac{a^{7}\sqrt x}{x^{5}} \right ] +
792\left[\frac{a^{6}}{x^{3}} \right ] +
792\left[\frac{a^{5}\sqrt x}{x^{2}} \right ] +
495\left[a^{4}\right ] +
220\left[a^{3}x\right ] +
66\left[a^{2}x ^{3}\right ] +
12\left[ax ^{4}\sqrt x \right ] +
1\left[x ^{6}]](/latexrender/pictures/822589d1bc387024c0d2716308a04aef.png)
E esta seria nossa criança...
Note que existe um termo com x elevado à quinta no denominador...
Não sei se este seria uma resposta aceitavel...
Como disse, rogo amparo aos mestres...
Um abraço
 no desenvolvimento de
no desenvolvimento de ![\left{\left(\frac{a}{x}+\sqrt[2]{x} \right)}^{12} \left{\left(\frac{a}{x}+\sqrt[2]{x} \right)}^{12}](/latexrender/pictures/1ebc74d7c40a039dd815f7812d01daae.png) , muito obrigado !
, muito obrigado ! x
x 

 no desenvolvimento de
no desenvolvimento de ![\left{\left(\frac{a}{x}+\sqrt[2]{x} \right)}^{12} \left{\left(\frac{a}{x}+\sqrt[2]{x} \right)}^{12}](/latexrender/pictures/1ebc74d7c40a039dd815f7812d01daae.png) , muito obrigado !
, muito obrigado ! x
x 

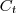 teremos:
teremos: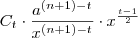
![C_t \cdot a \cdot x^{\frac{t-1}{2}-[(n+1)-t]} C_t \cdot a \cdot x^{\frac{t-1}{2}-[(n+1)-t]}](/latexrender/pictures/5d3f89a177ace73b162b7378924d2a09.png)
![\\
\frac{t-1}{2}-[(n+1)-t] = 5\\
\frac{t-1}{2}-[(12+1)-t] = 5\\
\frac{t-1}{2}-[13-t]=5\\
\frac{t-1}{2}-13+t=5\\
\frac{t}{2}+t-13-\frac{1}{2}=5\\
\frac{t+2t}{2}=5+13+\frac{1}{2}\\
\frac{3t}{2}=\frac{10+26+1}{2}\\
3t = 37\\
t = 37/3 \\
\frac{t-1}{2}-[(n+1)-t] = 5\\
\frac{t-1}{2}-[(12+1)-t] = 5\\
\frac{t-1}{2}-[13-t]=5\\
\frac{t-1}{2}-13+t=5\\
\frac{t}{2}+t-13-\frac{1}{2}=5\\
\frac{t+2t}{2}=5+13+\frac{1}{2}\\
\frac{3t}{2}=\frac{10+26+1}{2}\\
3t = 37\\
t = 37/3](/latexrender/pictures/b73f0b25e91a429209e0318fb4b950be.png)
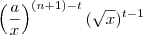
![\\
1\left[ \left (\frac{a}{x}\right )^{12}(\sqrt x)^0\right ] +
12\left[\left(\frac{a}{x} \right )^{11} (\sqrt x)^1 \right ] +
66 \left[\left(\frac{a}{x} \right )^{10} (\sqrt x)^2 \right ] +
220 \left[\left(\frac{a}{x} \right )^{9} (\sqrt x)^3 \right ] +
495 \left[\left(\frac{a}{x} \right )^{8} (\sqrt x)^4 \right ] +
792 \left[\left(\frac{a}{x} \right )^{7} (\sqrt x)^5 \right ] +
792 \left[\left(\frac{a}{x} \right )^{6} (\sqrt x)^6 \right ] +
792 \left[\left(\frac{a}{x} \right )^{5} (\sqrt x)^7 \right ] +
495 \left[\left(\frac{a}{x} \right )^{4} (\sqrt x)^8 \right ] +
220 \left[\left(\frac{a}{x} \right )^{3} (\sqrt x)^9 \right ] +
66 \left[\left(\frac{a}{x} \right )^{2} (\sqrt x)^{10} \right ] +
12 \left[\left(\frac{a}{x} \right )^{1} (\sqrt x)^{11} \right ] +
1 \left[\left(\frac{a}{x} \right )^{0} (\sqrt x)^{12} \right ] \\
1\left[ \left (\frac{a}{x}\right )^{12}(\sqrt x)^0\right ] +
12\left[\left(\frac{a}{x} \right )^{11} (\sqrt x)^1 \right ] +
66 \left[\left(\frac{a}{x} \right )^{10} (\sqrt x)^2 \right ] +
220 \left[\left(\frac{a}{x} \right )^{9} (\sqrt x)^3 \right ] +
495 \left[\left(\frac{a}{x} \right )^{8} (\sqrt x)^4 \right ] +
792 \left[\left(\frac{a}{x} \right )^{7} (\sqrt x)^5 \right ] +
792 \left[\left(\frac{a}{x} \right )^{6} (\sqrt x)^6 \right ] +
792 \left[\left(\frac{a}{x} \right )^{5} (\sqrt x)^7 \right ] +
495 \left[\left(\frac{a}{x} \right )^{4} (\sqrt x)^8 \right ] +
220 \left[\left(\frac{a}{x} \right )^{3} (\sqrt x)^9 \right ] +
66 \left[\left(\frac{a}{x} \right )^{2} (\sqrt x)^{10} \right ] +
12 \left[\left(\frac{a}{x} \right )^{1} (\sqrt x)^{11} \right ] +
1 \left[\left(\frac{a}{x} \right )^{0} (\sqrt x)^{12} \right ]](/latexrender/pictures/6869473ae78dd41f40f3582da1a09e88.png)
![\\
1\left[\frac{a^{12}\sqrt x ^{0}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x ^{1}}{x^{11}} \right ] +
66\left[\frac{a^{10}\sqrt x ^{2}}{x^{10}} \right ] +
220\left[\frac{a^{9}\sqrt x ^{3}}{x^{9}} \right ] +
495\left[\frac{a^{8}\sqrt x ^{4}}{x^{8}} \right ] +
792\left[\frac{a^{7}\sqrt x ^{5}}{x^{7}} \right ] +
792\left[\frac{a^{6}\sqrt x ^{6}}{x^{6}} \right ] +
792\left[\frac{a^{5}\sqrt x ^{7}}{x^{5}} \right ] +
495\left[\frac{a^{4}\sqrt x ^{8}}{x^{4}} \right ] +
220\left[\frac{a^{3}\sqrt x ^{9}}{x^{3}} \right ] +
66\left[\frac{a^{2}\sqrt x ^{10}}{x^{2}} \right ] +
12\left[\frac{a^{1}\sqrt x ^{11}}{x^{1}} \right ] +
1\left[\frac{a^{0}\sqrt x ^{12}}{x^{0}} \right ] \\
1\left[\frac{a^{12}\sqrt x ^{0}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x ^{1}}{x^{11}} \right ] +
66\left[\frac{a^{10}\sqrt x ^{2}}{x^{10}} \right ] +
220\left[\frac{a^{9}\sqrt x ^{3}}{x^{9}} \right ] +
495\left[\frac{a^{8}\sqrt x ^{4}}{x^{8}} \right ] +
792\left[\frac{a^{7}\sqrt x ^{5}}{x^{7}} \right ] +
792\left[\frac{a^{6}\sqrt x ^{6}}{x^{6}} \right ] +
792\left[\frac{a^{5}\sqrt x ^{7}}{x^{5}} \right ] +
495\left[\frac{a^{4}\sqrt x ^{8}}{x^{4}} \right ] +
220\left[\frac{a^{3}\sqrt x ^{9}}{x^{3}} \right ] +
66\left[\frac{a^{2}\sqrt x ^{10}}{x^{2}} \right ] +
12\left[\frac{a^{1}\sqrt x ^{11}}{x^{1}} \right ] +
1\left[\frac{a^{0}\sqrt x ^{12}}{x^{0}} \right ]](/latexrender/pictures/510bba62d9ecff8acca314885a6762dd.png)
![\\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}x}{x^{10}} \right ] +
220\left[\frac{a^{9}x\sqrt x}{x^{9}} \right ] +
495\left[\frac{a^{8}x ^{2}}{x^{8}} \right ] +
792\left[\frac{a^{7}x^2\sqrt x}{x^{7}} \right ] +
792\left[\frac{a^{6}x ^{3}}{x^{6}} \right ] +
792\left[\frac{a^{5}x ^{3}\sqrt x}{x^{5}} \right ] +
495\left[\frac{a^{4}x ^{4}}{x^{4}} \right ] +
220\left[\frac{a^{3}x ^{4}\sqrt x}{x^{3}} \right ] +
66\left[\frac{a^{2}x ^{5}}{x^{2}} \right ] +
12\left[\frac{ax ^{5}\sqrt x}{x^{1}} \right ] +
1\left[x ^{6}] \\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}x}{x^{10}} \right ] +
220\left[\frac{a^{9}x\sqrt x}{x^{9}} \right ] +
495\left[\frac{a^{8}x ^{2}}{x^{8}} \right ] +
792\left[\frac{a^{7}x^2\sqrt x}{x^{7}} \right ] +
792\left[\frac{a^{6}x ^{3}}{x^{6}} \right ] +
792\left[\frac{a^{5}x ^{3}\sqrt x}{x^{5}} \right ] +
495\left[\frac{a^{4}x ^{4}}{x^{4}} \right ] +
220\left[\frac{a^{3}x ^{4}\sqrt x}{x^{3}} \right ] +
66\left[\frac{a^{2}x ^{5}}{x^{2}} \right ] +
12\left[\frac{ax ^{5}\sqrt x}{x^{1}} \right ] +
1\left[x ^{6}]](/latexrender/pictures/00481cca490c4695528e654e7a4c34dd.png)
![\\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}}{x^{9}} \right ] +
220\left[\frac{a^{9}\sqrt x}{x^{8}} \right ] +
495\left[\frac{a^{8}}{x^{6}} \right ] +
792\left[\frac{a^{7}\sqrt x}{x^{5}} \right ] +
792\left[\frac{a^{6}}{x^{3}} \right ] +
792\left[\frac{a^{5}\sqrt x}{x^{2}} \right ] +
495\left[a^{4}\right ] +
220\left[a^{3}x\right ] +
66\left[a^{2}x ^{3}\right ] +
12\left[ax ^{4}\sqrt x \right ] +
1\left[x ^{6}] \\
1\left[\frac{a^{12}}{x^{12}} \right ] +
12\left[\frac{a^{11}\sqrt x }{x^{11}} \right ] +
66\left[\frac{a^{10}}{x^{9}} \right ] +
220\left[\frac{a^{9}\sqrt x}{x^{8}} \right ] +
495\left[\frac{a^{8}}{x^{6}} \right ] +
792\left[\frac{a^{7}\sqrt x}{x^{5}} \right ] +
792\left[\frac{a^{6}}{x^{3}} \right ] +
792\left[\frac{a^{5}\sqrt x}{x^{2}} \right ] +
495\left[a^{4}\right ] +
220\left[a^{3}x\right ] +
66\left[a^{2}x ^{3}\right ] +
12\left[ax ^{4}\sqrt x \right ] +
1\left[x ^{6}]](/latexrender/pictures/822589d1bc387024c0d2716308a04aef.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

