 por natanskt » Seg Dez 06, 2010 21:40
por natanskt » Seg Dez 06, 2010 21:40
DADO O BINOMIO
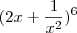
,DETERMINE:
A-)O TERMO INDEPENDENTE DE X
B-)O COEFICIENTE DO TERMO EM X^-3
TENTEI,E TENTEI MAIS NUM DA O RESULTADO PEDIDO,POR FAVOR SE ALGUEM FAZER PRA MIM NÃO SIMPLIFIQUE NADA,TO COM DUVIDA EM VARIAS PASSAGENS
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por alexandre32100 » Ter Dez 07, 2010 00:36
por alexandre32100 » Ter Dez 07, 2010 00:36
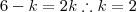
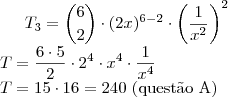
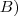
Se
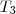
corresponde a
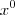
,

será equivalente a
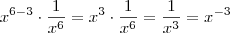
.
Encontre o valor de

.
-
alexandre32100
-
 por natanskt » Ter Dez 07, 2010 11:22
por natanskt » Ter Dez 07, 2010 11:22
cara eu num intendi acho que eu aprendi de modo diferente,dai não intendi.
mais a A eu conseguir fazer mais essa B,todos os exercicios que pede o coeficiente de tal numero eu num consigo fazer.
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por alexandre32100 » Ter Dez 07, 2010 22:58
por alexandre32100 » Ter Dez 07, 2010 22:58
-
alexandre32100
-
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Binômio de Newton
por Giordane Junior » Sex Dez 03, 2010 00:46
- 0 Respostas
- 8107 Exibições
- Última mensagem por Giordane Junior

Sex Dez 03, 2010 00:46
Binômio de Newton
-
- (PUC-PR)BINOMIO DE NEWTON
por natanskt » Seg Dez 06, 2010 10:54
- 1 Respostas
- 7389 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 11:54
Binômio de Newton
-
- Binômio de Newton
por natanskt » Seg Dez 06, 2010 12:07
- 1 Respostas
- 8816 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:07
Binômio de Newton
-
- Binomio de Newton.
por 380625 » Sex Mar 11, 2011 12:57
- 1 Respostas
- 3023 Exibições
- Última mensagem por MarceloFantini

Sex Mar 11, 2011 16:20
Binômio de Newton
-
- Binomio de newton
 por Fabricio dalla » Sex Abr 01, 2011 01:13
por Fabricio dalla » Sex Abr 01, 2011 01:13
- 8 Respostas
- 8430 Exibições
- Última mensagem por LuizAquino

Sáb Jul 23, 2011 19:12
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
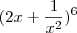 ,DETERMINE:
,DETERMINE:
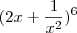 ,DETERMINE:
,DETERMINE:
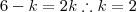
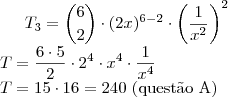
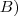
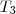 corresponde a
corresponde a 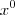 ,
,  será equivalente a
será equivalente a 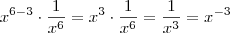 .
. .
.
 (
(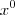 ) você faz
) você faz 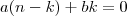 , onde
, onde  e
e  são, respectivamente as potências de x em cada termo.
são, respectivamente as potências de x em cada termo. ;
;  , portanto
, portanto  ;
;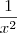 ;
; 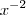 ; portanto
; portanto  ;
;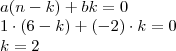
 seja
seja 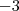 , portanto faça
, portanto faça  , ou ainda
, ou ainda 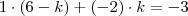 . Tendo estes valor basta aplicar a fórmula
. Tendo estes valor basta aplicar a fórmula 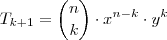 .
.
 é o grau da expressão;
é o grau da expressão; é a posição do termo;
é a posição do termo; é o grau do primeiro termo de
é o grau do primeiro termo de  dentro da expressão;
dentro da expressão; é o grau do segundo;
é o grau do segundo; é o grau que queremos para x;
é o grau que queremos para x;

 , avisa que eu resolvo.
, avisa que eu resolvo.

