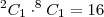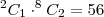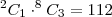Uma equipe de competição com 9 membros, sendo um coordenador
e seu adjunto, costuma expor seus projetos em eventos. Para
isso, a delegação enviada deve ser de no mínimo dois e no máximo
quatro componentes, sendo, pelo menos, um desses, o coordenador
ou o adjunto. O número de possibilidades de se compor cada delegação
é de
Eu tentei fazer combinação 9,2 . 9,4 mas nao deu certo