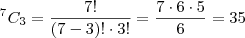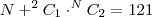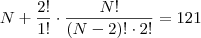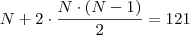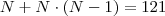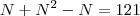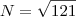Duvidas de A.COMBINATORIA

por **Mcastilho** » Qua Fev 29, 2012 20:51

Tenho duvida em 2 problemas de analise combinatoria.

1)Um fisioterapeuta recomendeu a um paciente que fizesse todos os dias 3 tipos diferentes de exercicios e lhe forneceu uma lista contendo 7 tipos diferentes de exercicios adequados a esse tratamento.Ao começar o tratamento o paciente resolve que a cada dia sua escolha dos 3 exercicios sera distinta sas escolhas feitas anteriormente.Onumero maximo de dias que o paciente podera manter esse procedimento é? RESPOSTA : 35

TENTEI FAZER C7,3 =40 MAS NAO ENTENDI

2)Sejam R e S 2 retas distintas e paralelas.Marcam se N pontos distintos P1,P2,P3,...,Pn sobre R e 2 pontos distintos Q1 e Q2 sobre S. O numero maximo de triangulos distintos que podem ser formados com vertices nesses N+2 pontos é 121. O numero N é igual a ? RESPOSTA : 11

Tentei fazer An+2,2 = 121 mas nao deu certo

por **joaofonseca** » Qua Fev 29, 2012 22:53

Em relação ao primeiro o pensamento está correto.As contas é que falharam.

$^7C_{3}=\frac{7!}{(7-3)! \cdot 3!}=\frac{7\cdot6\cdot5}{6}=35$

Em relação ao segundo:

Para formar um triangulo, são necessários 3 pontos não colineares( não podem fazer todos parte da mesma reta). assim temos duas situações:

-2 pontos da reta S e 1 ponto da reta R

-1 ponto da reta S e 2 pontos da reta R

Para a primeira situação temos que para o par de pontos da reta S podemos esconher N pontos da reta R.
Para a segunda situação podemos esconher 1 ponto da reta S entre os 2 dísponíveis, e para cada uma destas escolhas podemos esconher 2 pontos da reta R, entre os N disponíveis.As duas situações somadas têm de ser iguais a 121.Ou seja:

$N+^2C_{1} \cdot ^NC_{2}=121$

Desenvolvendo:

$N+\frac{2!}{1!} \cdot \frac{N!}{(N-2)! \cdot 2!}=121$

$N+2 \cdot \frac{N \cdot(N-1)}{2}=121$

$N+N\cdot(N-1)=121$
N+N^2-N=121