 por andersontricordiano » Qui Fev 02, 2012 17:56
por andersontricordiano » Qui Fev 02, 2012 17:56
Um dado é lançado duas vezes sucessivamente.Qual a probabilidade de não obtermos,em nenhum lançamento,os números 1 e 6?
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Qui Fev 02, 2012 23:35
por fraol » Qui Fev 02, 2012 23:35
Para dados equilibrados, podemos pensar de duas formas:
1) A probalidade de não sair nem 1 nem 6 nos dois lançamentos sucessivos é a probabilidade de sair quaisquer um dos outros 4 números no primeiro lançamento e a probabilidade de sair quaisquer um dos outros 4 números no segundo lançamento, isto é:
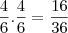
.
2) Ou usar o evento complementar, isto é a probabilidade pedida é igual a 1 menos a probabilidade de [sair 1 ou 6 no primeiro lançamento] ou { [sair um número diferente de 1 ou 6 no primeiro lançamento] e [sair 1 ou 6 no segundo lançamento ] } , assim:
![1 - \left[ \left( \frac{1}{6} + \frac{1}{6} \right) + \left( \frac{4}{36} + \frac{4}{36} \right) \right] = 1 - \frac{20}{36} = \frac{16}{36} 1 - \left[ \left( \frac{1}{6} + \frac{1}{6} \right) + \left( \frac{4}{36} + \frac{4}{36} \right) \right] = 1 - \frac{20}{36} = \frac{16}{36}](/latexrender/pictures/fdccf758098d2f3ec445a8bf0470e7b0.png)
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de probabilidade
 por Aquamarine » Sáb Fev 11, 2012 16:56
por Aquamarine » Sáb Fev 11, 2012 16:56
- 1 Respostas
- 1164 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 11, 2012 18:42
Estatística
-
- calculo das probabilidade estatistica
por Neta Silva » Seg Mai 12, 2014 01:19
- 0 Respostas
- 3999 Exibições
- Última mensagem por Neta Silva

Seg Mai 12, 2014 01:19
Estatística
-
- calculo das probabilidade estatistica
por Neta Silva » Seg Mai 12, 2014 01:20
- 0 Respostas
- 4108 Exibições
- Última mensagem por Neta Silva

Seg Mai 12, 2014 01:20
Probabilidade
-
- Cálculo de Probabilidade Condicionada P(xi|yj) - urgente
por adelino » Qui Mai 27, 2010 15:38
- 0 Respostas
- 1954 Exibições
- Última mensagem por adelino

Qui Mai 27, 2010 15:38
Estatística
-
- Cálculo da probabilidade - Solicito ajuda
por MARCION9 » Qui Mai 14, 2015 13:33
- 0 Respostas
- 2342 Exibições
- Última mensagem por MARCION9

Qui Mai 14, 2015 13:33
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



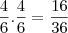 .
.![1 - \left[ \left( \frac{1}{6} + \frac{1}{6} \right) + \left( \frac{4}{36} + \frac{4}{36} \right) \right] = 1 - \frac{20}{36} = \frac{16}{36} 1 - \left[ \left( \frac{1}{6} + \frac{1}{6} \right) + \left( \frac{4}{36} + \frac{4}{36} \right) \right] = 1 - \frac{20}{36} = \frac{16}{36}](/latexrender/pictures/fdccf758098d2f3ec445a8bf0470e7b0.png) .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

