Para montar a senha de segurança de sua conta bancá-
ria, que deve ser formada por seis dígitos, João escolheu
1, 2, 5, 5, 7 e 8. Os dígitos escolhidos não serão dispostos
na ordem apresentada, pois, para João, é importante que
a senha seja um número maior do que 500.000.
Com os dígitos escolhidos por João, quantas senhas
maiores do que 500.000 podem ser formadas?
(A) 720
(B) 600
(C) 360
(D) 240
(E) 120


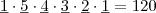
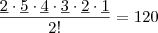


 .
.



