a)

b)
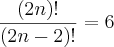
c)

d)

Respostas:
a)S=

b)S=

c)S=

d)S=



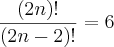







 e
e  .
.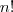 até
até  e cancele com o da direita, resolvendo a partir disso.
e cancele com o da direita, resolvendo a partir disso.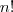 e no numerador expanda
e no numerador expanda  até
até  , ponha em evidência, expanda até o denominador e cancele, resolvendo o que sobrar.
, ponha em evidência, expanda até o denominador e cancele, resolvendo o que sobrar.

andersontricordiano escreveu:a)

andersontricordiano escreveu:b)

andersontricordiano escreveu:c)

andersontricordiano escreveu:d)



Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: