Bom, o método que sei é trabalhoso, mas no momento não to conseguindo lembrar de outro.
Caso esteja perguntando em relação as setas:
Considerando que todas as setas apontam na direção de X, vamos contar os casos:
de Y pra Z há 2 modos
de R pra Z há 1 modo direto
há
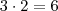
modos indo por Y
de S pra Z há 2 modos diretos
há
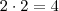
modos indo por Y
de X pra Z há 3 modos indo por R direto
há
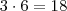
modos indo por R e Y
há 2 modos indo por Y
há 6 modos indo por S
há

modos indo por S e Y
Portanto, há 3+18+2+6+12=41 modos diferentes.
Caso esteja perguntando em relação as casas, então podemos ter as ligações
XRZ, XRYZ, XYZ, XSYZ e XSZ, ou seja, 5 ligações diferentes.
Só os loucos sabem...



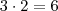 modos indo por Y
modos indo por Y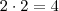 modos indo por Y
modos indo por Y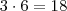 modos indo por R e Y
modos indo por R e Y modos indo por S e Y
modos indo por S e Y

 .
.



