1) Num certo colégio, 4% dos homens e 1% das mulheres têm mais de 1,75m de altura. 60% dos estudantes são mulheres, Um estudante escolhido ao acaso e tem mais de 1,75m de altura. Qual a probabilidade de que seja homem?
fiz assim:
P(h/+1,75) =
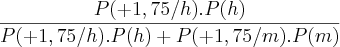
P(h/+1,75) = [Unparseable or potentially dangerous latex formula. Error 6 ]
p(h/+1,75) = 72,73%
2) A probabilidade de que um indivíduo da classe A comprar um carro é de
 , da B é de
, da B é de  e da C é de
e da C é de  . As probabilidades de os indivíduos comprarem um carro da marca
. As probabilidades de os indivíduos comprarem um carro da marca  sao
sao  ,
,  e [Unparseable or potentially dangerous latex formula. Error 6 ], dado que sejam de A, B e C, respectivamente. Certa loja vendeu um carro da marca
e [Unparseable or potentially dangerous latex formula. Error 6 ], dado que sejam de A, B e C, respectivamente. Certa loja vendeu um carro da marca  . Qual a probabilidade de que o indivíduo que o comprou seja da classe B?
. Qual a probabilidade de que o indivíduo que o comprou seja da classe B?fiz assim:
P(B/X) =
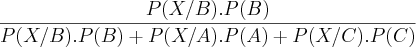
P(B/X) =
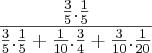
P(B/X) =

3) hÁ 60 candidatos a um emprego. alguns têm curso superior(S), outros não; alguns tem no minimo tres anos de experiencia (T), outros não. A distribuição é:
S S' total
T 12 6 18
T' 24 18 42
total 36 24 60
Se a ordem de entrevista é aleatória, S é o evento: o primeiro a se entrevistado tem curso superior e T é o evento: o primeiro tem experiencia minima de tres anos. Calcular as seguintes probabilidades:
a) P(T/S)
P(T/S) =

P(T/S) =
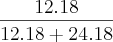
P(T/S) =

b) P(S
 T)
T)P(S
 T) = P(S).P(T)
T) = P(S).P(T)P(S
 T) = 36.18
T) = 36.18P(S
 T) = 648
T) = 648c) P(S'P(S
 T)
T)P(S'P(S
 T) = P(S').P(T)
T) = P(S').P(T)P(S'P(S
 T) = 24.18
T) = 24.18P(S'P(S
 T) = 432
T) = 432d) P(S)
P(S) =
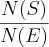
P(S) =

P(S) =

4) Em uma industria de enlatados, as linhas de produção, I, II e III respondem por 50%, 30% e 20% da produção respectivamente. As proporções de latas com defeito de produção nas linhas I, II e III são 0,4%, 0,6% e 1,2%. Qual a probabilidade de uma lata defeituosa (descoberta no final da inspeção do produto acabado) provir da linha I?
P(I/D) =
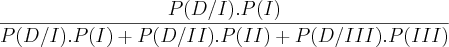
P(I/D) =
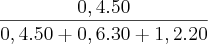
P(I/D) = 32,26%
BOM, TUDO ISSO, AHSUHUSA...
BJOS
E AGRADEÇO DESDE JA


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
