por Suy Becker » Qua Mai 11, 2011 10:29
por Suy Becker » Qua Mai 11, 2011 10:29
Por favor, alguém poderia me ajudar??
não to conseguindo fazer de jeito nenhum esses 2 exercicios da minha lista. 1º Não entendi nada do enunciado e 2º Não consegui saber que fórmula usar.
1. Qual o número de jogadas de uma moeda necessário para assegurar uma probabilidade superior a 0,75 de se obter ao menos uma cara (K)?
2. Uma tábua de mortalidade acusa as seguintes taxas de mortalidade

(isto é, probabilidade de um indivíduo de idade

morrer antes de atingir a idade

+ 1):
(tabela a seguir)
x 30 31 32 33 34 35
q 0,00213 0,00219 0,00225 0,00232 0,0024 0,00251
a) Dado um indivíduo de 30 anos, qual a probabilidade dele atingir a idade de 31 anos?
b) Para o mesmo indivíduo, qual a probabilidade de morrer antes de completar 35 anos?
POR FAVOR ME AJUDEMMM...\
Obrigadaa
-
Suy Becker
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Fev 25, 2011 14:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Publicidade e Propaganda
- Andamento: cursando
 por carlosalesouza » Qua Mai 11, 2011 12:55
por carlosalesouza » Qua Mai 11, 2011 12:55
Olá...
O 1º é muito simples...
Sabemos que a probabilidade de NÃO ocorrer cara, é
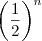
, onde n é o número de vezes que vc lançar a moeda... assim, a probabilidade de ocorrer cara(k) é
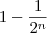
Aqui, sabemos que p(k) = 0,75 = 3/4
Então:

Quanto ao outro... a probabilidade de atingir uma tal idade é a probabilidade de não morrer... ou seja...

De 30 pra 31 não dá nem graça... rs é 1 - 0,00213...
Até 35 é a mesma coisa: 1 - 0,00213 - 0,00219 - 0,00225 - 0,00232 ..........
Ok?
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Suy Becker » Qua Mai 11, 2011 15:11
por Suy Becker » Qua Mai 11, 2011 15:11
MUITO OBRIGADA
XD
-
Suy Becker
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Fev 25, 2011 14:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Publicidade e Propaganda
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidade - Confirmar resultados Urgentee
por Suy Becker » Qua Mai 11, 2011 15:04
- 0 Respostas
- 8493 Exibições
- Última mensagem por Suy Becker

Qua Mai 11, 2011 15:04
Estatística
-
- urgentee
por jean » Dom Nov 30, 2008 20:02
- 1 Respostas
- 1304 Exibições
- Última mensagem por Molina

Seg Dez 01, 2008 00:39
Pedidos
-
- É URGENTEE! SOBRE CILINDROS!
por Bianca » Ter Set 08, 2009 13:37
- 1 Respostas
- 3950 Exibições
- Última mensagem por Molina

Ter Set 08, 2009 19:03
Geometria Plana
-
- Transformação linear! URGENTEE
por manuoliveira » Qua Nov 07, 2012 15:26
- 2 Respostas
- 1547 Exibições
- Última mensagem por manuoliveira

Qua Nov 07, 2012 22:23
Álgebra Elementar
-
- mais um questão URGENTEE
por my2009 » Qua Set 16, 2015 13:08
- 2 Respostas
- 3539 Exibições
- Última mensagem por my2009

Ter Nov 17, 2015 11:58
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (isto é, probabilidade de um indivíduo de idade
(isto é, probabilidade de um indivíduo de idade  morrer antes de atingir a idade
morrer antes de atingir a idade  + 1):
+ 1):

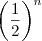 , onde n é o número de vezes que vc lançar a moeda... assim, a probabilidade de ocorrer cara(k) é
, onde n é o número de vezes que vc lançar a moeda... assim, a probabilidade de ocorrer cara(k) é