Oi pessoal fera em Matemática. Tô tentando resolver uma questão que acho ser Anál. comb.
34. O número de subconjunto de A = {1, 2, 3, 4} que contém ou elemento 2 ou o elemento 3 é:
resposta: 12
Eu não consegui chegar esse número, eu encontrei.
(2),(1,2),(2,4),(1,2,4)
(3),(1,3),(3,4),(1,3,4)
8 combinações. Faltou 4.



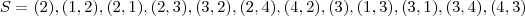
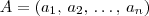 é uma n-upla ordenada, isto é, um ponto em
é uma n-upla ordenada, isto é, um ponto em  . Já
. Já 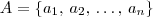 é um conjunto com
é um conjunto com 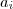 é distinto dos outros para que o conjunto tenha
é distinto dos outros para que o conjunto tenha