Galera preciso que me ajudem a resolver esse exercício:1. Considere o espaço amostral do lançamento de um dado e a observação da face superior.
Descreva, por seus elementos, os seguintes eventos:
a) A: sair face par; b) B: sair face primo;
c) C: sair face maior que 3; d) D: sair face maior que 6;
e) E: sair face múltipla de 3; f) F: sair face menor ou igual a 4;
2. O experimento consiste em lançar dois dados e observar a soma dos pontos das faces superiores. Determine o espaço amostral.
3. O experimento consiste em lançar dois dados e observar a diferença dos pontos das faces superiores. Determine o espaço amostral do experimento.
4. O experimento consiste em lançar dois dados e observar o produto dos pontos das faces superiores. Determine o espaço amostral do experimento.
5. O experimento consiste em lançar dois dados e observar em módulo, a diferença dos pontos das faces superiores. Determine o espaço amostral do experimento.
6. O experimento consiste em lançar três moedas e observar a diferença entre o número de caras e o número de coroas obtidos neste lançamento.
7. O experimento consiste em retirar duas cartas de um baralho comum e anotar ordenadamente os naipes destas cartas. Determine o espaço amostral do experimento.
.
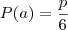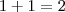e o maior 
, dentre estes temos todas as possibilidades.
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.