01. De quantos modos diferentes se poder organizar, em uma fila de 10 cadeiras, 4 palmeirenses, 3 atleticanos, 2 flamenguistas e 1 gremista, de modo que torcedores da mesma fiquem sempre juntos e palmeirenses não fiquem nas extremidades?
Tentei resolvê-la da seguinte forma;
Primeiro pensei nas possibilidades de organização dos torcedores dentro de seus respectivos grupos de torcida. Portanto, conclui isto:
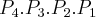, representando, respectiviamente, palmeirenses, atleticanos, flamenguistas e o gremista. Compactanto minha idéia, pensei nas possibilidades de estruturação entre as torcidadas retirando os palmeirenses das extremidades, cheguei a esse resultado: 
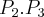. Sendo o produto de tudo (
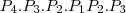) igual a 3456. Entretanto, foi considerado errado.Por favor ajudem-me, desde já obrigado.
.
