Em um setor de uma empresa existem 15 funcionários. Dentre esses, uma funcionária se chama Silvia e, dos 7 homens, Paulo, é um deles. Deseja-se formar comissões constituidas de 5 mulheres e 4 homens. Então, o número de comissões de que Paulo participa sem Sílvia é?
A resposta sería 420.
Alguém pode me ajudar com a resolução?
Obrigado.


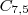 = 21
= 21 = 20
= 20

 .
.
 :
: