 por Douglasm » Seg Fev 15, 2010 10:38
por Douglasm » Seg Fev 15, 2010 10:38
Bom dia a todos do fórum! Gostaria de saber se alguém pode me ajudar com essa questão:
Considere um polígono convexo com
n lados e suponha que não há duas de suas diagonais paralelas, nem três que concorram num mesmo ponto que não seja vértice.
- Quantos são os pontos de intersecção interiores ao polígono?
- Quantos são os pontos de intersecção exteriores ao polígono?
Principalmente na parte em que se pede os pontos exteriores, eu tenho dificuldades em estipular como funcionaria isso. Imagino que quando falamos dos pontos interiores, estamos apenas nos referindo a uma combinação de
n, quatro a quatro (quatro pontos = duas diagonais = um ponto de intersecção). A resposta dessa até confere com o gabarito, mas gostaria que alguém me explicasse com mais clareza! =)
As respostas:
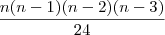
e

, respectivamente.
Desde já agradeço.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- diagonais de um poligono
por alfabeta » Seg Mar 26, 2012 21:24
- 1 Respostas
- 2198 Exibições
- Última mensagem por Anniemf

Qua Mar 28, 2012 15:05
Geometria Plana
-
- Número de diagonais e lados de um polígono
por Ana Carolina Caetano » Sáb Mar 03, 2012 15:48
- 5 Respostas
- 4095 Exibições
- Última mensagem por LuizAquino

Sáb Mar 03, 2012 22:14
Geometria Plana
-
- [Combinação de Numeros]Combinação até chegar em outro
por moacirrf » Dom Set 30, 2012 15:51
- 0 Respostas
- 1781 Exibições
- Última mensagem por moacirrf

Dom Set 30, 2012 15:51
Análise Combinatória
-
- Diagonais de um heptágono por combinatória?
por EngenheiroErick » Dom Set 04, 2016 00:07
- 0 Respostas
- 5803 Exibições
- Última mensagem por EngenheiroErick

Dom Set 04, 2016 00:07
Análise Combinatória
-
- [Polígonos convexos: ângulos e diagonais] - IBMEC
por vihmc » Seg Fev 24, 2014 15:53
- 0 Respostas
- 4199 Exibições
- Última mensagem por vihmc

Seg Fev 24, 2014 15:53
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
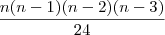 e
e  , respectivamente.
, respectivamente. 
