Consideraremos que as cartas são escolhidas
simultaneamente.
Por definição,

, onde

é o número de casos em que o evento

acontece e
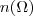
é o número de casos possíveis.
Seja
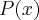
a probabilidade de que esteja escrita uma letra (A,J ou Q) dentre as cartas escolhidas;
Calculemos
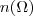
:
Basta calcular o número de combinações das
dez cartas tomadas
duas a duas, isto é:
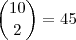
Calculemos
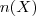
:
i)Considerando que uma das cartas é o "A", a outra carta escolhida pode ser uma das restantes, assim:
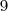
combinações.
ii)Considerando que uma das cartas é o "J", a outra carta escolhida pode ser umas das oito restantes já que contabilizamos o par (A,J) no item anterior. Assim:
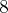
combinações.
iii)Considerando que uma das cartas é o "Q", analogamente teremos

combinações.
Assim,

Por fim,
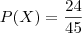
, isto é,

Uma nota importante é que, se considerarmos a ordem em que as cartas são escolhidas, isto é, as cartas não são escolhidas simultaneamente, obteremos outro valor, conforme abaixo:
Como todas a escolha de qualquer carta é equiprovável, temos:
Na primeira carta, a probabilidade de escolher "A,Q,J" é
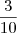
Na segunda carta, a probabilidade de escolher "A,Q,J" é

porque uma dentre essas foi escolhida anteriormente.
Assim,
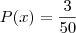



 , onde
, onde  é o número de casos em que o evento
é o número de casos em que o evento  acontece e
acontece e 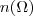 é o número de casos possíveis.
é o número de casos possíveis.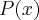 a probabilidade de que esteja escrita uma letra (A,J ou Q) dentre as cartas escolhidas;
a probabilidade de que esteja escrita uma letra (A,J ou Q) dentre as cartas escolhidas;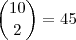
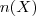 :
: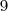 combinações.
combinações.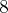 combinações.
combinações. combinações.
combinações.
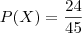 , isto é,
, isto é, 
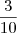
 porque uma dentre essas foi escolhida anteriormente.
porque uma dentre essas foi escolhida anteriormente.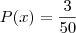


 .
.



