Primeiramente desculpe a pergunta idiota,mais estou tendo sérios problemas em um trabalho.
Tenho dois vetores de amostas aleatórias, que eu denominei x e y, com 38 pontos cada um, cada vetor corespondendo a uma variável aleatória V.A. de distribuição desconhecida.
Para cada valor de
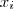do vetor x eu preciso calcular a probabilidade condicional com um valor 
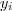do vetor y. Já tentei de algumas formas mais ainda não saí do lugar.Eu já sei da relação da razão da interseção entre x e y pela probabilidade de y, mais não consigo aplicar. para o caso dos dois vetores de V.A.
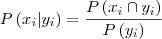
Será que alguem poderia me ajudar.
Abraços
Adelino
adelinocpp@gmail.com
por 
.
