Idades (anos) Freqüência Acumulada
14 2
15 4
16 9
17 12
18 15
19 18
20 20
Um desses jovens será escolhido ao acaso. Qual a probabilidade de que o jovem escolhido tenha menos de 18 anos,
sabendo que esse jovem terá 16 anos ou mais?
(A) 8/14 (B) 8/16 (C) 8/20 (D) 3/14 (E) 3/16
tentativa de resolução
Espaço amostra de A {14,15,16,17,18,19}
evento de A tenha menos de 18 e terá 16 anos ou mais
Condição B {16,17,18}
A
=
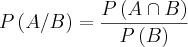Cheguei ao resultado de 3/7- porem o resultado da questão é 8/14
Ja o exercicio de nr 02 tambem não cheguei a conclusão
Uma das medidas de dispersão é a variância populacional, que é calculada por
. Sabendo-se que m é a média aritmética dessas idades, qual a variância das idades na população formada pelos 20 jovens?Tentei a resolução
média aritimetica
14+15+16+17+18+19 = 99/6 = 16,50 anos
6
Porem a questão da variância não sei como fazer, alguem poderia me ajudar???
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.