Seja n o número total de anagramas da palavra
BOTAFOGO, que contêm as 4 consoantes em ordem
alfabética. O valor de n é igual a:
(A) 520
(B) 280
(C) 480
(D) 340
Por favor, gostaria muito de ver a resolução!!!



Pri Ferreira escreveu:Seja n o número total de anagramas da palavra
BOTAFOGO, que contêm as 4 consoantes em ordem
alfabética. O valor de n é igual a:
(A) 520
(B) 280
(C) 480
(D) 340
 possibilidades.
possibilidades.
 pq dá 1 sobre alguma coisa...
pq dá 1 sobre alguma coisa... , já que são 3 os e 1 a, é isso msm???
, já que são 3 os e 1 a, é isso msm???
Pri Ferreira escreveu:Nessa questão ainda naum entendi uma coisa...Isso está certo:pq dá 1 sobre alguma coisa...
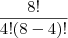 .
.Pri Ferreira escreveu:E na permutação com repetição o q encontrei foi, já que são 3 os e 1 a, é isso msm???
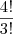 anagramas.
anagramas.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



