 por Aquamarine » Sáb Fev 11, 2012 16:56
por Aquamarine » Sáb Fev 11, 2012 16:56
Toda as afirmativas sao corretas,
mas eu nao entendi como o tipo A eh igual a 32%
se 68% nao eh A então entendi que seria do tipo O
esses 68
E o restante 3% seria A
ia ser meio estranho mas nao entendi os 32 %
- Anexos
-

-
Aquamarine
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Fev 06, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Fev 11, 2012 18:42
por MarceloFantini » Sáb Fev 11, 2012 18:42
Se alguém não é do tipo sanguíneo A, isto significa que ela pode ser do tipo B, do tipo O ou do tipo AB. Em termos de probabilidade,
não ser do tipo A significa ser pertencer a
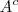
, ou seja, A complementar. E daí sabemos que
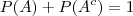
, logo se 68% não são do tipo A, teremos
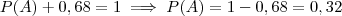
que é 32%.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de probabilidade
por andersontricordiano » Qui Fev 02, 2012 17:56
- 1 Respostas
- 1294 Exibições
- Última mensagem por fraol

Qui Fev 02, 2012 23:35
Estatística
-
- calculo das probabilidade estatistica
por Neta Silva » Seg Mai 12, 2014 01:19
- 0 Respostas
- 4000 Exibições
- Última mensagem por Neta Silva

Seg Mai 12, 2014 01:19
Estatística
-
- calculo das probabilidade estatistica
por Neta Silva » Seg Mai 12, 2014 01:20
- 0 Respostas
- 4108 Exibições
- Última mensagem por Neta Silva

Seg Mai 12, 2014 01:20
Probabilidade
-
- Cálculo de Probabilidade Condicionada P(xi|yj) - urgente
por adelino » Qui Mai 27, 2010 15:38
- 0 Respostas
- 1954 Exibições
- Última mensagem por adelino

Qui Mai 27, 2010 15:38
Estatística
-
- Cálculo da probabilidade - Solicito ajuda
por MARCION9 » Qui Mai 14, 2015 13:33
- 0 Respostas
- 2342 Exibições
- Última mensagem por MARCION9

Qui Mai 14, 2015 13:33
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



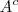 , ou seja, A complementar. E daí sabemos que
, ou seja, A complementar. E daí sabemos que 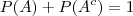 , logo se 68% não são do tipo A, teremos
, logo se 68% não são do tipo A, teremos 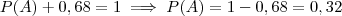 que é 32%.
que é 32%.


 .
.



