 por joaofonseca » Qua Jan 11, 2012 20:36
por joaofonseca » Qua Jan 11, 2012 20:36
No calculo combinatorio existe o que se chama de arranjo simples (sem repetição)
A notação é:

, em que

.
Depois existe o que se chama de arranjo composto (com repetição).
A notação é:

Mas julgo que nem sempre o
n e o
p são o mesmos em ambos os casos.
Exemplo #1:
Quantos números de 3 algarismos se podem formar com os digitos 0 e 1?
Aqui aplica-se um arranjo composto, em que
n=2 e
p=3.
Exemplo #2:
Numa competição participam 3 jogadores.Só existe prémio para o 1º e 2º lugares. De quantas formas diferentes se podem distribuir os prémios?
Aqui aplica-se um arranjo simples, em que
n=3 e
p=2.
Porque isto acontece?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Arkanus Darondra » Qua Jan 11, 2012 21:00
por Arkanus Darondra » Qua Jan 11, 2012 21:00
Olá joaofonseca,
exemplo#1: Como você mesmo colocou, quando pode haver repetição, usa-se o arranjo composto.
Logo, como o exercício não diz que os números devem ser formados por algarismos distintos, e nem poderia (ele dá 2 algarismos e pede números compostos por 3), usa-se a o arranjo composto.
Obs: Creio que neste caso, como o número não pode começar por 0, teremos 4 números
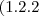
e não
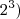
.
exemplo#2: Como uma pessoa não pode ocupar dois lugares no pódio ao mesmo tempo, usa-se a arranjo simples.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por joaofonseca » Qua Jan 11, 2012 21:30
por joaofonseca » Qua Jan 11, 2012 21:30
No 1º exemplo eu estava-me a referir em numeração binária, do tipo 010,100 ou 001.
O porque de aplicar um arranjo simples ou arranjo composto eu sei. A questão é porque o valor de n e p não terem o mesmo valor apesar de nas notações respetivas estarem nas mesmas posições.
Existem casos em que n e p têm o mesmos valores, quer se trate de um arranjo simples, ou arranjo composto.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Arkanus Darondra » Qua Jan 11, 2012 21:49
por Arkanus Darondra » Qua Jan 11, 2012 21:49
joaofonseca escreveu:No 1º exemplo eu estava-me a referir em numeração binária, do tipo 010,100 ou 001.
Certo. Na minha observação eu apenas supus, afinal o enunciado não especifica (Arranjo de n p a p)
joaofonseca escreveu:A questão é porque o valor de n e p não terem o mesmo valor apesar de nas notações respetivas estarem nas mesmas posições.
Existem casos em que n e p têm o mesmos valores, quer se trate de um arranjo simples, ou arranjo composto.
Imagine que n é um valor que você vai "arranjar" e p é algo fixo.
No
exemplo#1 o fato de ter que formar números de 3 algarismos é algo fixo, o que será "arranjado" é a ordem dos algarismos dados.
Então,
n = 2 e p = 3No
exemplo#2 o fato que existir premiação para os 1º e 2º colocados na competição é fixo, o que será "arranjado" é a forma de como os prêmios serão distribuídos entre os jogadores.
Então
n = 3 e p = 2
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo combinatorio
por joaofonseca » Seg Jan 16, 2012 23:18
- 1 Respostas
- 1888 Exibições
- Última mensagem por fraol

Seg Jan 16, 2012 23:56
Desafios Difíceis
-
- Calculo combinatório
por joaofonseca » Sáb Mai 05, 2012 10:00
- 5 Respostas
- 2888 Exibições
- Última mensagem por Fabiano Vieira

Dom Mai 06, 2012 23:43
Polinômios
-
- Cálculo de notação vetorial e trabalho usando intg. de linha
por Fernandobertolaccini » Ter Fev 03, 2015 12:43
- 1 Respostas
- 1643 Exibições
- Última mensagem por Russman

Ter Fev 03, 2015 19:07
Cálculo: Limites, Derivadas e Integrais
-
- DILEMA COMBINATÓRIO!
por jorge1986 » Qua Jul 01, 2009 11:23
- 4 Respostas
- 4089 Exibições
- Última mensagem por jorge1986

Qua Jul 29, 2009 15:39
Estatística
-
- [ED] Notação
por Jhenrique » Sex Mai 10, 2013 17:25
- 0 Respostas
- 1459 Exibições
- Última mensagem por Jhenrique

Sex Mai 10, 2013 17:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , em que
, em que  .
.


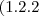 e não
e não 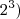 .
.