Olá
Andersonvrum. Em primeiro lugar, melhore o título de seus tópicos, não utilize termos nada significativos com o conteúdo como "ajuda etc", além de melhor organizar o fórum, cria destaque para quem se interessa pelo assunto e sua ajuda pode ser mais rápida.
Veja nossos "primeiros passos".
Sobre sua dúvida, cuidado com a expressão "no mínimo", significa o mesmo que "pelo menos". Ou seja, para obter a probabilidade procurada

, será necessário calcular

Podemos representar com anagramas utilizando as seguintes letras:

para cara e
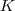
para coroa.
Ao calcular
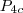
, você deve notar que é necessário saber o número de anagramas possíveis neste caso:
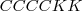
E ainda, para cada lançamento a probabilidade é

.
Antes, estude como calcular o número de anagramas com elementos repetidos.
Por exemplo para
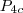
você terá:
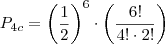
Escreva seus progressos e eventuais dúvidas para

e

.
Bons estudos!


 , será necessário calcular
, será necessário calcular
 para cara e
para cara e 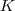 para coroa.
para coroa.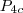 , você deve notar que é necessário saber o número de anagramas possíveis neste caso:
, você deve notar que é necessário saber o número de anagramas possíveis neste caso: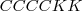
 .
.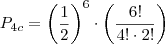
 e
e  .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

