 por pogalski » Dom Jun 05, 2011 11:03
por pogalski » Dom Jun 05, 2011 11:03
Estou tentando desenvolver esse exercicio, mas nao consigo chegar a um resultado, nao entendo a fórmula usada.
1. Uma companhia planejou apresentações de vendas para dez clientes importantes. A
probabilidade de receber um pedido como resultado de tal apresentação é estimada em 0,4.
a) Qual é a probabilidade de não receber nenhum pedido como resultado das apresentações?
b) Qual é a probabilidade de todos os dez clientes realizarem pedidos em decorrência da
apresentação realizada?
c) Qual é a probabilidade de receber três ou mais pedidos como resultado das
apresentações?
-
pogalski
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 05, 2011 10:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciências contabeis
- Andamento: cursando
 por Neperiano » Ter Jun 21, 2011 16:34
por Neperiano » Ter Jun 21, 2011 16:34
Ola
Voce tenque usar a probabilidade binomial, se naum souber usar responda q ajudo
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qua Jun 22, 2011 00:47
por MarceloFantini » Qua Jun 22, 2011 00:47
Vamos denominar por X a quantidade de pedidos como resultado das apresentações. Na item (a), temos:

Item (b) é análogo:
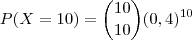
No item (c), temos que pensar um pouco diferente. A probabilidade pedida é

, que é igual a pensar todos os casos menos os que não atendem: quando 2 pedidos são feitos, apenas 1 ou nenhum. Logo:


Não domino completamente o assunto, mas acredito que as resoluções sejam assim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- varíaveis aleatórias contínuas conjuntas
por gprestes » Qua Nov 24, 2010 08:38
- 0 Respostas
- 2535 Exibições
- Última mensagem por gprestes

Qua Nov 24, 2010 08:38
Estatística
-
- Probabilidade-variaveis aleatórias - Help
por benni » Dom Mai 08, 2011 12:03
- 2 Respostas
- 4243 Exibições
- Última mensagem por psdias

Ter Mai 22, 2012 09:42
Probabilidade
-
- [Probablidade] variáveis aleatórias
por 1paulo » Sáb Mai 17, 2014 13:06
- 0 Respostas
- 2222 Exibições
- Última mensagem por 1paulo

Sáb Mai 17, 2014 13:06
Probabilidade
-
- Prova com Variáveis Aleatórias Independentes
 por EREGON » Seg Mai 18, 2015 09:02
por EREGON » Seg Mai 18, 2015 09:02
- 0 Respostas
- 1273 Exibições
- Última mensagem por EREGON

Seg Mai 18, 2015 09:02
Probabilidade
-
- [Variáveis Aleatórias] Esperança Matemática
 por guisore_09 » Ter Dez 29, 2015 08:58
por guisore_09 » Ter Dez 29, 2015 08:58
- 4 Respostas
- 11073 Exibições
- Última mensagem por guisore_09

Dom Jan 03, 2016 10:20
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




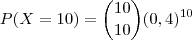
 , que é igual a pensar todos os casos menos os que não atendem: quando 2 pedidos são feitos, apenas 1 ou nenhum. Logo:
, que é igual a pensar todos os casos menos os que não atendem: quando 2 pedidos são feitos, apenas 1 ou nenhum. Logo:








