Olá
heroncius!
Você já deve ter percebido que este problema é semelhante àquele dos bombons.
A interpretação do enunciado é fundamental para montar o
sistema de equações.
Vamos então, representar este
sistema:
Nomeando as variáveis:
S: número de selos
F: número de folhas
colocando-se 20 selos em cada folha, sobram 02 folhas;
A equação dita aqui, é:
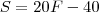
colocando-se 15 selos em cada folha, todas as folhas são ocupadas e ficam sobrando ainda 60 selos.
E aqui:

Então, novamente temos um
sistema com duas equações e duas incógnitas:

Temos vários caminhos para resolvê-lo. Vamos subtrair a segunda equação da primeira:
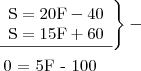


Substituindo
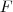
em qualquer uma das duas equações, encontramos que

.
Podemos verificar a coerência destes valores, testando no enunciado.
Espero ter ajudado!
Abraço.


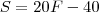


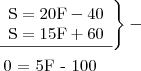


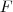 em qualquer uma das duas equações, encontramos que
em qualquer uma das duas equações, encontramos que  .
.