 por Molina » Qui Jul 30, 2009 22:55
por Molina » Qui Jul 30, 2009 22:55
Ta aí Rodrigo...
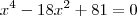
Considerando

, temos:
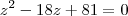
.
.
.
resolvendo por Baskhara ou Soma e Porduto temos as raízes:
z'=9 e z''=9Agora voltamos na primeira consideração que fizemos:


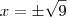
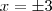 S={-3,+3}
S={-3,+3}Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equação BIQUADRADA
por Jaison Werner » Ter Jan 04, 2011 16:56
- 3 Respostas
- 3413 Exibições
- Última mensagem por Dan

Sex Jan 07, 2011 19:42
Cálculo
-
- Equação Biquadrada
por Flavio Cacequi » Sex Abr 20, 2018 07:30
- 0 Respostas
- 2176 Exibições
- Última mensagem por Flavio Cacequi

Sex Abr 20, 2018 07:30
Equações
-
- [Equação biquadrada]
por amandasousa_m » Dom Jul 21, 2013 19:02
- 2 Respostas
- 1705 Exibições
- Última mensagem por amandasousa_m

Seg Jul 22, 2013 10:34
Equações
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7729 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13234 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
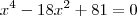
 , temos:
, temos: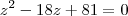


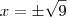
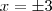


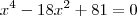
 , temos:
, temos: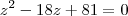


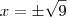
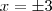




 , avisa que eu resolvo.
, avisa que eu resolvo.

