Raphael Feitas10 escreveu:Para construir um muro,João levaria 30 dias e Carlos levaria 25 dias. Os dois começam a trabalhar juntos,mas após 6 dias João deixa o trabalho, 2 dias após a saida deste, Carlos também abandona. Antônio sozinho, consegue terminá-lo em 24 dias. Para realizar a construção do muro sozinho, Antônio levaria. R: 50 dias
Rafhael,
fiz assim:
Considerando

o muro 100% construído
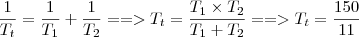
Esse valor encontrado (acima), representa o tempo total que João e Carlos levariam juntos para construir o muro;
Apliquemos uma regra de três simples para determinar o quanto o muro foi construído pelos dois em 6 dias; chamei de

.
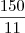
dias ----------------------

6 dias -----------------------------

(dir.)
Teremos
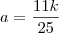
Ou seja, nos 6 dias de trabalho João e Carlos construíram
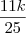
do muro, resta-nos saber quanto falta do muro. Portanto,
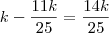
Depois de 2 dias Carlos abandona, então o raciocínio é análogo ao anterior, só que, com os números de Carlos, veja:

---------------------- 25 dias

---------------------- 2 dias
(dir.)
Teremos
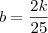
Isto é, trabalhando sozinho Carlos levantou
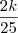
do muro, calculemos quanto falta para terminar o muro:
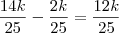
Daí,
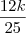
---------------------- 24 dias

-------------------------

(dir.)

Espero ter ajudado!
Retorne em caso de dúvidas.
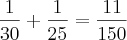
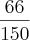
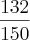
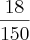 que equivale á 24 dias, pra fazer o serviço todo vai dá achei 200 mais ñ bate com a resposta...
que equivale á 24 dias, pra fazer o serviço todo vai dá achei 200 mais ñ bate com a resposta...

 o muro 100% construído
o muro 100% construído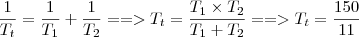
 .
.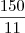 dias ----------------------
dias ---------------------- 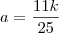
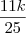 do muro, resta-nos saber quanto falta do muro. Portanto,
do muro, resta-nos saber quanto falta do muro. Portanto,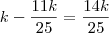
 ---------------------- 2 dias
---------------------- 2 dias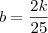
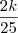 do muro, calculemos quanto falta para terminar o muro:
do muro, calculemos quanto falta para terminar o muro: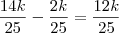
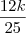 ---------------------- 24 dias
---------------------- 24 dias


 .
. ,
,  e para
e para  ,
,  .
.
 .
.
