Considere que três pessoas, Pedro, Carlos e João tem a seguinte relação entre seus salários:
i – Duas vezes o salário de Carlos, menos o salário de João, menos o salário de Pedro é igual a R$ 3000,00.
ii – A soma do salário das três pessoas é igual a R$ 6000,00.
iii – O salário de Pedro, mais duas vezes o salário de João, mais duas vezes o salário de Carlos é igual a R$ 11000,00.
a) Escreva o sistema de equações que representa a relação entre os salários de Pedro, Carlos e João.
b) Escreva a matriz ampliada (ou aumentada) do sistema de equações obtido no item anterior
c) Através do escalonamento da matriz ampliada, reescreva o sistema de equações na forma matricial de maneira que a matriz dos coeficientes esteja na forma triangular superior.
d) Com o resultado do item anterior, obtenha os salários de Pedro, Carlos e João





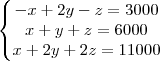

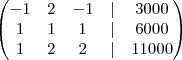
 , fica:
, fica: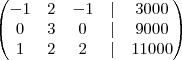
 , fica:
, fica: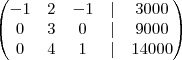
 , fica:
, fica:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)