 por TAE » Sex Jun 01, 2012 00:00
por TAE » Sex Jun 01, 2012 00:00
Boa noite, só uma pequena dúvida o porquê de não estar dando b=-2.
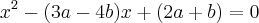
. Raízes da equação 3 e 4. Determine a e b.

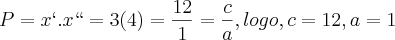
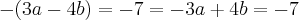

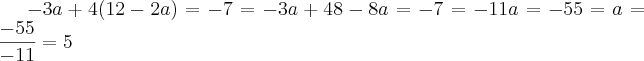

Resposta:
a=5
b=2
Valeu.
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
 por Russman » Sex Jun 01, 2012 01:34
por Russman » Sex Jun 01, 2012 01:34
Você deve montar um sistema!

Agora, resolva-o!
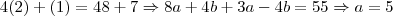
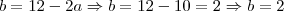
Veja que aplicando estes valores na equação obtemos
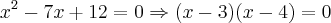
cuja solução é
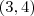
, como se qeria!
Você fez certo! Porqe teria de calcular

?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por TAE » Sex Jun 01, 2012 16:57
por TAE » Sex Jun 01, 2012 16:57
Foi mal pela, confusão é o que o livro está dando b=-2, então o gabarito deve estar errado, muito obrigado pela ajuda.
“O tolo, quando erra,queixa-se dos outros; o sábio queixa-se de si mesmo.” (Sócrates, 469-399, AC).
-
TAE
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Mar 20, 2012 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: TÉC. ELETRÔNICA
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar a Equação da Hiperbole...
por Mystic_Fan » Ter Jun 07, 2011 23:49
- 1 Respostas
- 1536 Exibições
- Última mensagem por DanielFerreira

Qui Jun 16, 2011 16:45
Geometria Analítica
-
- [circunferência] determinar a equação
por Fabio Wanderley » Qui Abr 26, 2012 11:23
- 1 Respostas
- 3223 Exibições
- Última mensagem por LuizAquino

Qui Abr 26, 2012 16:16
Geometria Analítica
-
- [Determinar equação da Parábola]
 por aliceleite » Ter Set 04, 2012 20:20
por aliceleite » Ter Set 04, 2012 20:20
- 1 Respostas
- 1537 Exibições
- Última mensagem por Russman

Qua Set 05, 2012 01:31
Funções
-
- [ Determinar a equação do plano]
por lucasdemirand » Dom Set 01, 2013 00:12
- 0 Respostas
- 668 Exibições
- Última mensagem por lucasdemirand

Dom Set 01, 2013 00:12
Álgebra Linear
-
- Determinar equação da elipse
por fernandabalvin » Qua Mar 08, 2017 15:36
- 0 Respostas
- 2058 Exibições
- Última mensagem por fernandabalvin

Qua Mar 08, 2017 15:36
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
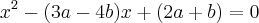 . Raízes da equação 3 e 4. Determine a e b.
. Raízes da equação 3 e 4. Determine a e b.
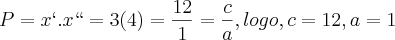
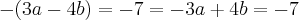

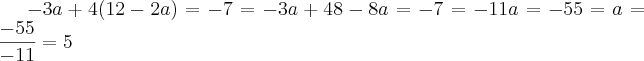


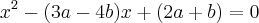 . Raízes da equação 3 e 4. Determine a e b.
. Raízes da equação 3 e 4. Determine a e b.
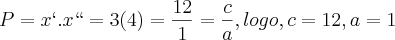
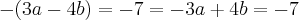

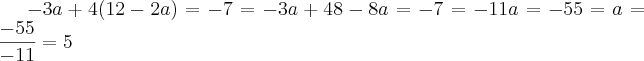



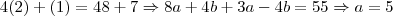
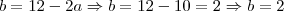
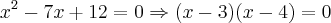
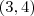 , como se qeria!
, como se qeria! ?
?

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.