 por Matheus Lacombe O » Sex Fev 24, 2012 11:23
por Matheus Lacombe O » Sex Fev 24, 2012 11:23
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Fev 24, 2012 12:55
por MarceloFantini » Sex Fev 24, 2012 12:55
Vou multiplicar tudo por 10 e vejamos como a equação fica:
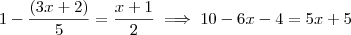
.
Daí,
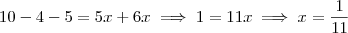
.
Você esqueceu de distribuir o sinal na primeira fração.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Sex Fev 24, 2012 13:10
por Neperiano » Sex Fev 24, 2012 13:10
Ola
Outro forma de resolver
1 - ((3x+2)/5) = (x+1)/2
passa o 2 pro lado
2+((-6x-4)/5)=x+1
passa o 2 pro outro lado
(-6x-4)/5=x-1
passa o 5 pro outro lado
-6x-4=5x-5
isola o x
1=11x
x = 1/11
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [equação modular] resultado confuso
por jvabatista » Qua Abr 18, 2012 02:05
- 2 Respostas
- 1564 Exibições
- Última mensagem por jvabatista

Qua Abr 25, 2012 23:22
Álgebra Elementar
-
- [Resolvido][Equação] Com fração.
por replay » Sex Mar 01, 2013 17:02
- 2 Respostas
- 1078 Exibições
- Última mensagem por replay

Sex Mar 01, 2013 19:25
Álgebra Elementar
-
- Equação Logaritmica com fração
por Rangelgec » Ter Dez 01, 2015 15:59
- 1 Respostas
- 5331 Exibições
- Última mensagem por Gebe

Ter Dez 08, 2015 02:15
Logaritmos
-
- equação do segundo grau com fração
por hevhoram » Sex Abr 20, 2012 12:08
- 1 Respostas
- 3694 Exibições
- Última mensagem por Cleyson007

Sex Abr 20, 2012 12:30
Sistemas de Equações
-
- Como montar a equação contendo Fração e porcentagem
por macedo1967 » Sáb Set 23, 2017 14:16
- 3 Respostas
- 12942 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:20
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





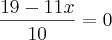

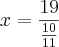
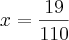
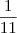


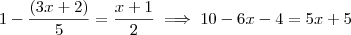 .
.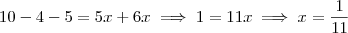 .
.

