por Aprendizmatematica » Sex Fev 17, 2012 17:03
Pedro gasta 1/5 de seu salário líquido com transporte e 3/10 com moradia, ainda sobram R$ 243,00 para as outras despesas. O salário líquido de Pedro em reais é igual a:
Como eu estou tentando fazer e está dando errado:
Primeira forma: x - 1/5 - 3/10 + 243 = Tirei o mmc de 5 e 10
10x - 2 -3 - 2.430 / 10
10x=2.435
x = 2.435 / 10 Resposta errada pois a divisão não dá exada = 243,000
Tentei de outra forma que deu a mesma coisa: 243 + x = 1/5 - 3/10 (mmc )
243/10 + x/10 = 2/10 - 3/10
2.430 + x = 2-3
-1 = 2430 +10x
isolar o x: 10x = 2430-1 também não existe uma divisão exata.... o resultado que tenho como verdadeiro é: R$ 486,00
-
Aprendizmatematica
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Sex Fev 17, 2012 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Comunicação Social
- Andamento: formado
por LuizAquino » Sex Fev 17, 2012 19:13
Aprendizmatematica escreveu:Pedro gasta 1/5 de seu salário líquido com transporte (...)
Se x é o salário líquido de Pedro, então ele gasta
com transporte.
Aprendizmatematica escreveu:(...) e 3/10 com moradia (...)
Ou seja, ele gasta
com moradia.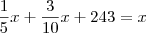
Aprendizmatematica escreveu:(...) ainda sobram R$ 243,00 para as outras despesas. (....)
Ou seja, podemos dizer que o salário líquido de Pedro está separado em três partes:
para transporte,
para moradia e uma sobra de R$ 243,00.
Aprendizmatematica escreveu:O salário líquido de Pedro em reais é igual a:
Basta resolver a equação:
Agora tente terminar o exercício.
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
por Aprendizmatematica » Sex Fev 17, 2012 19:24
Nossa, parece tão óbvio agora, mas meu problema sempre será a interpretação... Muito obrigada mesmo!!! Agora consegui.!!!!!!!!
-
Aprendizmatematica
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Sex Fev 17, 2012 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Comunicação Social
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do primeiro grau
por isaiaspereira » Qui Jan 27, 2011 00:53
- 3 Respostas
- 2714 Exibições
- Última mensagem por Elcioschin
Qui Jan 27, 2011 14:02
Álgebra Elementar
-
- Equação do primeiro grau
por Netu » Sáb Jan 19, 2013 20:20
- 1 Respostas
- 1396 Exibições
- Última mensagem por DanielFerreira
Sáb Jan 19, 2013 20:41
Equações
-
- Problemas de equação do primeiro grau.
por Andrewo » Seg Fev 20, 2012 08:55
- 2 Respostas
- 5536 Exibições
- Última mensagem por Andrewo
Seg Fev 20, 2012 11:35
Sistemas de Equações
-
- Problemas de equação do primeiro grau.
por Andrewo » Qui Fev 23, 2012 18:00
- 3 Respostas
- 4354 Exibições
- Última mensagem por LuizAquino
Sex Fev 24, 2012 10:56
Sistemas de Equações
-
- Problemas de equação do primeiro grau III
por Andrewo » Seg Fev 27, 2012 11:58
- 3 Respostas
- 3990 Exibições
- Última mensagem por MarceloFantini
Ter Fev 28, 2012 16:04
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
