[Sistemas Lineares] Precisão do Método de Gauss-Seidel

por **VFernandes** » Qui Out 06, 2011 13:50

Caros amigos, primeiramente peço desculpas se o assunto foge um pouco do tema, mas foi a seção mais adequada que encontrei.
Tenho o seguinte problema em minhas mãos:
$\begin{pmatrix} 4 & -1 & 0 \\ -2 & 3 & -1 \\ -1 & -3 & 5 \end{pmatrix} \begin{pmatrix} {x}_{1}} \\ {x}_{2}} \\ {x}_{3}} \end{pmatrix} = \begin{pmatrix} 2\\ 0 \\ 1 \end{pmatrix}$
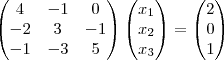
Calcule uma iteração por Gauss-Seidel, partindo de = (0,0,0) e estime quantas iterações são necessárias para que se atinja a precisão $\epsilon$ = 0.0001
Bom, vamos lá:

${{x}_{1}}^{1} = \frac{1}{4}(2-(-1)\times0-0\times0)) = 0,5$
${{x}_{2}}^{1} = \frac{1}{3}(0-(-2)\times0,5-(-1)\times0)) = 0,33$
${{x}_{3}}^{1} = \frac{1}{5}(1-(-1)\times0,5-(-3)\times0,33)) = 0,5$

$\beta_1 = \frac{1}{4}(1+0) = 0,25$
$\beta_ = \frac{1}{3}(2\times0,25+1) = 0,5$
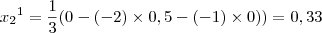
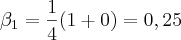
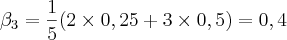$\beta_3 = \frac{1}{5}(2\times0,25+3\times0,5) = 0,4$ portanto,
M = 0.5 (maior dos betas)
Até aqui, sem problemas, a questão vem agora:
Sabemos que:
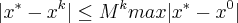$|x^*-x^k|\leq M^k max|x^*-x^0|$ portanto,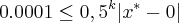
$0.0001\leq 0,5^k |x^*-0|$
o que não nos ajuda em muito, pois não sabemos x* (valor exato de x)
Alguma alma caridosa saberia como lidar com isso? Será que temos que delimitar um intervalo onde está contida a solução do sistema?

[Sistemas Lineares] Precisão do Método de Gauss-Seidel

[Sistemas Lineares] Precisão do Método de Gauss-Seidel

[Sistemas Lineares] Precisão do Método de Gauss-Seidel

Quem está online