por ALF » Sex Ago 26, 2011 13:24
por ALF » Sex Ago 26, 2011 13:24
Dado o Sistema:
ax + 2y + z = 0
2x + ay - z = 1 - a
x + y + z = 1
Ao tentar resolvê-lo por castilho cheguei no seguinte resultado:
1.
a² -a - 3 = 0
a = 1 +-
![\sqrt[2]{13} \sqrt[2]{13}](/latexrender/pictures/ac068c680e0ca056ee420dba2b49fde9.png)
/ 2
2. a² =3
Resposta correta: Não admite solução para 3 valores de a.
-
ALF
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Ago 26, 2011 12:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Dom Ago 28, 2011 12:57
por LuizAquino » Dom Ago 28, 2011 12:57
Qual é o texto completo do exercício?
Temos o sistema:
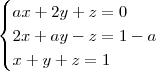
Para que o sistema não possua solução alguma, ele deve ser impossível. Para isso acontecer, a matriz dos coeficientes deve ter determinante nulo e alguma das matrizes das incógnitas deve ter determinante não nulo. Em resumo, deve ocorrer det(D) = 0 e det(Dx), det(Dy) ou det(Dz) diferente de zero.
Nesse exercício, a matriz dos coeficientes é:

Por outro lado, a matriz da incógnita x é:

Agora termine de analisar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sistema linear com 4 variaveis e 3 equaçoes
por rhcruz » Dom Mai 06, 2012 11:07
- 2 Respostas
- 7165 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 16:01
Sistemas de Equações
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3092 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema Linear] com duas equações e três icógnitas
por Billie » Seg Ago 27, 2012 21:31
- 3 Respostas
- 3981 Exibições
- Última mensagem por DanielFerreira

Ter Ago 28, 2012 19:26
Sistemas de Equações
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5564 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- Sistema linear
por kael » Ter Out 20, 2009 14:14
- 1 Respostas
- 2673 Exibições
- Última mensagem por kael

Ter Out 20, 2009 16:24
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{13} \sqrt[2]{13}](/latexrender/pictures/ac068c680e0ca056ee420dba2b49fde9.png) / 2
/ 2
![\sqrt[2]{13} \sqrt[2]{13}](/latexrender/pictures/ac068c680e0ca056ee420dba2b49fde9.png) / 2
/ 2