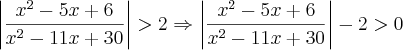por Caroline Oliveyra » Dom Jul 10, 2011 13:03
por Caroline Oliveyra » Dom Jul 10, 2011 13:03
Oie!
Gente, eu to com uma dúvida aqui a respeito de uma inequação que envolve soma de módulos. A inequação é:
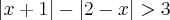
.
Eu não estou conseguindo fazer essa soma. Tentei aplicar as propriedae de módulo, mas o x anulou... Tenho um monte de questões assim pra resolver, mas tô meio perdida. Eu sempre coloco aqui o modo como eu tentei resolver, mas é que dessa vez eu não tô nem sabendo começar...

Tem um outro tipo de inequação modular aqui que eu também não tô sabendo fazer... Acho que meu problema é com o módulo!!

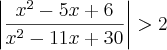
Se alguém puder me ajudar agredeço muitíssimo!!
Se puder colocar a resolução completa pra eu poder acompanhar também agradeço muito!!!

Beijos!!
"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
 por giulioaltoe » Dom Jul 10, 2011 21:27
por giulioaltoe » Dom Jul 10, 2011 21:27
na primeira inequação ao igualar a equação tanto pro < -3 quanto pro >3 e um dos casos voce tira o modulo no sinal oposto, e nesse caso ele nao se anula, assim vai achar um resultado, se o outro resultado X se anula e porque so tem a imagem pra um dos valores, e nao pros dois!
a segunda inequação e so aplicar as condiçoes de existencia... fazer um calculo pra (inequação)>2 e outro para (inequação)<-2 :P
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por MarceloFantini » Seg Jul 11, 2011 04:16
por MarceloFantini » Seg Jul 11, 2011 04:16
Giulio, não é bem assim. Note que há dois módulos, portanto não se deve fazer isso. Como proceder:
1) Analise os sinais dos módulos individualmente:

é zero quando
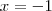
, positivo quando

e negativo quando
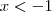

é zero quando

, positivo quando
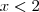
e negativo quando

2) Monte os intervalos e teste:
Primeiro intervalo:

Portanto nesse primeiro intervalo não existe solução.
Segundo intervalo:
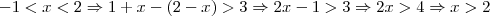
Novamente resultado inválido.
Terceiro intervalo:
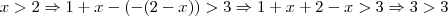
Outra afirmação inválida.
Pelo que notei, não existe intervalo onde está inequação esteja satisfeita. Tem certeza que digitou certo? Para conferir digitei no wolfram e também disse que era falsa.
Na segunda inequação, procure achar as raízes das equações e analise quando a fração é positiva ou negativa, repetindo os passos: veja os intervalos e teste quais os que tem respostas válidas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por giulioaltoe » Ter Jul 12, 2011 00:11
por giulioaltoe » Ter Jul 12, 2011 00:11
essa questao so possui resposta de uma das equaçoes, ta na minha lista de exercicio tbm

-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por giulioaltoe » Ter Jul 12, 2011 01:45
por giulioaltoe » Ter Jul 12, 2011 01:45
a resolução ai... nao fiz a resolução da outra condiçao pois o delta da negativo sendo assim nao existe imagem... o valor fica meio quabrado mas acredito que seja isso!!
- Anexos
-

-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por Caroline Oliveyra » Ter Jul 12, 2011 14:30
por Caroline Oliveyra » Ter Jul 12, 2011 14:30
Oi!!
Obrigada!! Eu vou ver aki se acompanho o raciocínio e resolvo!!!
Beijos pros dois!! =D
"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
 por MarceloFantini » Ter Jul 12, 2011 15:24
por MarceloFantini » Ter Jul 12, 2011 15:24
Giulio, novamente o modo de resolver não é este. Siga os passos que eu disse: analise o sinal de

para depois verificar caso a caso e retirar o módulo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caroline Oliveyra » Qua Jul 13, 2011 14:56
por Caroline Oliveyra » Qua Jul 13, 2011 14:56
Oi Marcelo!
A primeira equação eu entendi como faz,obrigada!!
Na segunda é que eu ainda não acompanhei seu raciocínio. Você tirou o módulo antes de fazer as operações com a fração? Pelo que eu entendi do seu desenvolvimento você passou o 2 para o primeiro membro, subtraindo-o da fração modular:
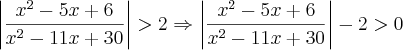
Eu não entendi porque depois daí você tirou o módulo. O resto eu entendi, mas não sei que propriedade você usou pra tirar o módulo da fração. No seu desenvolvimento eu não consegui perceber como você fez isso... Você poderia me explicar?

Beijos e obrigada de novo!!
"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
 por LuizAquino » Qua Jul 13, 2011 15:52
por LuizAquino » Qua Jul 13, 2011 15:52
Olá Caroline Oliveyra,
Para sanar suas dúvidas, eu recomendo que você revise o conteúdo de inequações modulares.
Um lugar interessante de começar a sua revisão é no canal do Nerckie no YouTube:
http://www.youtube.com/nerckieProcure pelas vídeo-aulas "Matemática - Aula 27 - Inequação Modular".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Caroline Oliveyra » Qua Jul 13, 2011 16:22
por Caroline Oliveyra » Qua Jul 13, 2011 16:22
Minha internet é discada... =(
Mas obrigada, eu vou ver se assisto esse vídeo em algum lugar! kkkkkkkkkkkkk
"... então não importa se você é antílope ou leão; amanheceu, comece a correr."
-
Caroline Oliveyra
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Jun 19, 2011 13:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Metalúrgica e de Materiais
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequações quocientes com módulos
por Jader Martim » Qui Abr 23, 2015 23:23
- 0 Respostas
- 2029 Exibições
- Última mensagem por Jader Martim

Qui Abr 23, 2015 23:23
Inequações
-
- Subtração de modulos, em uma inequação
por ferrazrafael » Qua Set 01, 2010 15:35
- 1 Respostas
- 3895 Exibições
- Última mensagem por MarceloFantini

Qua Set 01, 2010 20:52
Funções
-
- Dificuldade com limites e módulos
por Luisags » Qui Abr 12, 2012 23:05
- 5 Respostas
- 3828 Exibições
- Última mensagem por gabriel feron

Ter Abr 17, 2012 03:17
Cálculo: Limites, Derivadas e Integrais
-
- resolver inequaçao com modulos
por rodrigonapoleao » Qua Dez 19, 2012 22:40
- 1 Respostas
- 1636 Exibições
- Última mensagem por e8group

Qui Dez 20, 2012 20:00
Equações
-
- [Matematica Aplicada]-Modulos entre outros.
por Hellsius » Seg Fev 27, 2012 15:30
- 1 Respostas
- 1470 Exibições
- Última mensagem por -Rafael-

Qua Fev 29, 2012 13:19
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
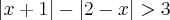 .
.

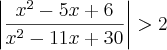




 é zero quando
é zero quando 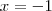 , positivo quando
, positivo quando  e negativo quando
e negativo quando 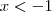
 é zero quando
é zero quando  , positivo quando
, positivo quando 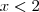 e negativo quando
e negativo quando 

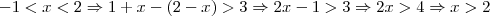
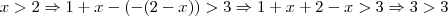


 para depois verificar caso a caso e retirar o módulo.
para depois verificar caso a caso e retirar o módulo.