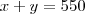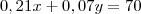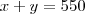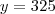por Kelvin Brayan » Sáb Abr 23, 2011 13:19
(UFG) Para se deslocar de casa até seu trabalho, um trabalhador percorre 550 km por mês. Para isso, em alguns dias, ele utiliza um automóvel e, em outros, uma motocicleta. Considerando que o custo do quilômetro rodado é de 21 centavos para o automóvel e de 7 centavos para a motocicleta, CALCULE quantos quilômetros o trabalhador deve andar em cada um dos veículos, para que o custo total mensal seja de R$ 70,00.
-
Kelvin Brayan
- Colaborador Voluntário
-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
-
SidneySantos
- Usuário Dedicado
-
- Mensagens: 28
- Registrado em: Qua Abr 20, 2011 07:47
- Localização: Belém - Pará
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educaçao Matemática
- Andamento: cursando
por Kelvin Brayan » Dom Abr 24, 2011 10:40
Obrigado !
-
Kelvin Brayan
- Colaborador Voluntário
-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Outro Problema
por gabimucedola » Ter Mar 30, 2010 01:15
- 3 Respostas
- 2129 Exibições
- Última mensagem por gabimucedola
Ter Mar 30, 2010 12:55
Álgebra Elementar
-
- OUTRO PROBLEMA..
por gabimucedola » Sex Abr 02, 2010 18:07
- 1 Respostas
- 1193 Exibições
- Última mensagem por estudandoMat
Sáb Abr 03, 2010 01:16
Matemática Financeira
-
- Outro problema
por gabimucedola » Dom Abr 04, 2010 23:35
- 1 Respostas
- 1456 Exibições
- Última mensagem por estudandoMat
Seg Abr 05, 2010 01:33
Matemática Financeira
-
- outro problema de mat
por Andersonborges » Qui Mar 03, 2011 00:24
- 1 Respostas
- 1424 Exibições
- Última mensagem por Abelardo
Qui Abr 14, 2011 20:18
Funções
-
- problema de matematica
por verinha72 » Qua Out 06, 2010 23:24
- 1 Respostas
- 3480 Exibições
- Última mensagem por Elcioschin
Qui Out 07, 2010 17:57
Mensagens Matemáticas
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
