 por Dan » Ter Fev 01, 2011 14:39
por Dan » Ter Fev 01, 2011 14:39
Oi gente.
Eu resolvi o seguinte sistema de equações lineares:

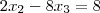
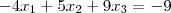
O sistema tem uma solução, que é (29, 16, 3).
Então eu pensei nessa solução como um ponto em
R³, e em cada equação como uma reta em
R³, que se encontram no ponto (29, 16, 3).
Daí o que eu fiz foi determinar um ponto qualquer para cada uma das equações, e obtive (2,1,0), (0,8,1) e (2,-2,1). Acredito que esteja na ordem da primeira à terceira equação.
Em seguida fiz a equação paramétrica de cada reta, obtendo primeiro o vetor (diminuindo o ponto qualquer de cada reta da solução do sistema) e em seguida montando cada equação:
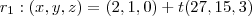
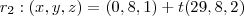

E por último joguei tudo no Winplot que fez o seguinte gráfico (clique na imagem para ampliar):

Eu girei e aproximei esse gráfico em todos os sentidos, e pelo gráfico eu fico seguro em afirmar que sim, as três retas se cruzam.
Agora, o que eu quero confirmar é se o procedimento e o raciocínio fazem sentido. Eu cheguei ao objetivo final que eu queria, que era ver as três retas se cruzando, mas em poucas palavras, equações lineares podem ser transformadas em equações paramétricas dessa forma? E o ponto onde elas se cruzam é realmente a solução do sistema
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Dan » Ter Fev 01, 2011 14:53
por Dan » Ter Fev 01, 2011 14:53
Era pra ter saído um ponto de interrogação por último "E o ponto onde elas se cruzam é realmente a solução do sistema?".
Desculpem o novo post, não estou conseguindo carregar o tópico e editar a mensagem.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Fev 02, 2011 10:38
por LuizAquino » Qua Fev 02, 2011 10:38
Sua interpretação está equivocada.
Um sistema linear de 3 equações e 3 incógnitas é visto geometricamente como o ponto de interseção entre três
planos, e não entre três retas.
Lembre-se que uma equação do tipo
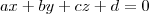
representa um plano no

, e não uma reta.
O que você fez foi para cada plano determinar uma reta sobre ele que passa pelo ponto (29, 16, 3). Obviamente, por sua construção a interseção entre essas retas será esse ponto.
Aproveito ainda para dar uma sugestão. Que tal experimentar um programa livre para traçar seus gráficos? O endereço é:
http://www.geogebra.orgSe você quiser um curso ensinando a usar este programa, visite:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Dan » Qua Fev 02, 2011 11:25
por Dan » Qua Fev 02, 2011 11:25
Obrigado LuizAquino. Eu já uso o GeoGebra, mas dispensei ele nessa oportunidade porque ele ainda não traça gráficos em R³, certo?
Mas o seu canal é muito bom, parabéns. Com certeza vou usar seus vídeos quando eu tiver alguma dúvida de construção no GeoGebra.
Perfeito, de fato essas são equações de planos. Agora consegui pensar em uma maneira como eles três se cortam com um ponto em comum.
Obrigado novamente.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qua Fev 02, 2011 11:37
por LuizAquino » Qua Fev 02, 2011 11:37
Dan escreveu:Eu já uso o GeoGebra, mas dispensei ele nessa oportunidade porque ele ainda não traça gráficos em R³, certo?
Nativamente, ainda não. Mas, podemos construir um usando os conhecimentos de Geometria Analítica. Veja o vídeo:
20. Curso de GeoGebra - Objetos Tridimensionaishttp://www.youtube.com/watch?v=FfCwo666dHA
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3419 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equaçoes parametricas
por angels900 » Ter Jan 31, 2012 14:35
- 6 Respostas
- 3709 Exibições
- Última mensagem por LuizAquino

Ter Jan 31, 2012 17:04
Geometria Analítica
-
- Equações paramétricas da curva
por kalschne » Qui Fev 16, 2012 20:51
- 3 Respostas
- 2107 Exibições
- Última mensagem por kalschne

Qui Fev 16, 2012 22:48
Geometria Analítica
-
- [Equações Paramétricas - Espaço]
por raimundoocjr » Ter Set 24, 2013 20:40
- 2 Respostas
- 1856 Exibições
- Última mensagem por raimundoocjr

Qua Set 25, 2013 19:05
Cálculo: Limites, Derivadas e Integrais
-
- Geometria Analítica Equações Paramétricas.
por lucat28 » Sex Set 16, 2011 19:08
- 1 Respostas
- 1400 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 19:43
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

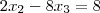
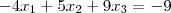
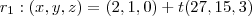
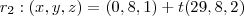




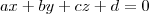 representa um plano no
representa um plano no  , e não uma reta.
, e não uma reta.