Certo trabalho pode ser feito em 44 dias, por uma turma de 15 operários, trabalhando 8h/d. Depois de 10 dias, 5 operários deixam de trabalhar e o restante passa a trabalhar 9h/d. No fim de quanto tempo o trabalho fica terminado? resp. 45 dias e 3h
44d ------------------ 15op ------------- 8h/d
(44 - 10)d ----------(15 - 5)op -------- 9h/d
Se em 44 dias executam todo o trabalho, façamos:
44d ----------- k
Em 10 dias executaram...
44d --------- k
10d -------- ?
44? = 10k
? = 10k/44 (executaram essa fração do trabalho em 10 dias)
Daí,
44d -------------- 15op --------------------- 8h/d ------------------- k
x -- -------------- 10op --------------------- 9h/d ------------------- (k - 10k/44)
______________(inv)________________(inv)_______________(dir)
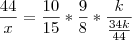



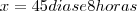


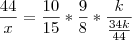



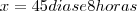


 .
.
 :
: