 por aline2010 » Dom Ago 08, 2010 07:46
por aline2010 » Dom Ago 08, 2010 07:46
O polinômio 2x^3-9x^2+12x+1
a)tem três raízes distintas
b)tem uma raíz dupla
c)tem duas raízes duplas
d)tem uma raiz tripla
e)n.r.a
-
aline2010
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Jun 13, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matmática
- Andamento: formado
 por MarceloFantini » Seg Ago 09, 2010 06:08
por MarceloFantini » Seg Ago 09, 2010 06:08

. Como

,
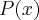
tem uma raíz no intervalo
![[-1,0] [-1,0]](/latexrender/pictures/f5ca84f050ce8ce1ca50cf1e97edd83a.png)
. Na primeira derivada:

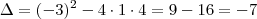
Como
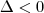
, a reta tangente ao gráfico não é horizontal em nenhum ponto, portanto não há outras raízes, visto que é um polinômio de grau ímpar.
Alternativa E.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8111 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2568 Exibições
- Última mensagem por mottasky

Qui Set 15, 2011 15:52
Álgebra Elementar
-
- raízes.
por carolina camargo » Qua Jun 17, 2009 16:39
- 5 Respostas
- 2951 Exibições
- Última mensagem por Molina

Qua Jun 17, 2009 19:01
Funções
-
- raizes
por cristina » Qui Set 09, 2010 09:57
- 3 Respostas
- 1860 Exibições
- Última mensagem por MarceloFantini

Qui Set 09, 2010 17:52
Números Complexos
-
- RAIZES
por vanessitah » Sáb Mar 05, 2011 20:36
- 12 Respostas
- 6458 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 13:48
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Como
. Como  ,
, 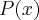 tem uma raíz no intervalo
tem uma raíz no intervalo ![[-1,0] [-1,0]](/latexrender/pictures/f5ca84f050ce8ce1ca50cf1e97edd83a.png) . Na primeira derivada:
. Na primeira derivada:
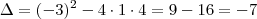
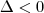 , a reta tangente ao gráfico não é horizontal em nenhum ponto, portanto não há outras raízes, visto que é um polinômio de grau ímpar.
, a reta tangente ao gráfico não é horizontal em nenhum ponto, portanto não há outras raízes, visto que é um polinômio de grau ímpar.

