 por Lorenzo » Qui Jun 17, 2010 22:41
por Lorenzo » Qui Jun 17, 2010 22:41
Estou com problemas em aritmética modular, por isso estou enviando esta pergunta:
(OBM) Encontre todos os inteiros a > 0 e b > 0 tais que:
4 . 3^a = 11+ 5^b
Na resolução percebi que é analisada a equação módulo 5. Assim:
4 . 3^a = 1 (mod 5) O problema é agora, daí conclui-se que "a" é par, e depois(em outra análise) que "b" também é par, só que eu não entendo como se da essa conclusão. Talvez haja alguma propriedade que não conheço. Por favor explique com detalhes.
-
Lorenzo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 13, 2010 21:12
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: pretendo engenharia civil
- Andamento: cursando
 por Tom » Sex Jul 02, 2010 23:28
por Tom » Sex Jul 02, 2010 23:28
Desejamos encontrar as soluções naturais

para a equação
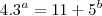
Ora,
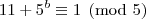
, para todo

. Logo
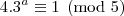
e como

é inversível a
 módulo cinco
módulo cinco, então devemos ter
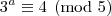
Analisando a
congruência módulo cinco para as potências de três, temos:
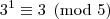
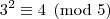
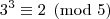
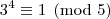
A partir daí as potências vão deixando os mesmos resíduos de modo a concluirmos que:
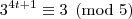
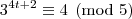
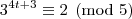
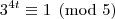
Assim, como
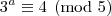
, então :
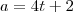
, com
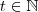
; que equivale a
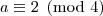
, isto é,

é par!
Analisemos a equação à luz
da congruência em módulo três: Para satisfazer a igualdade devemos ter
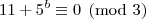
, isto é,
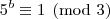
Analisando a
congruência módulo três para as potências de cinco, temos:
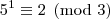
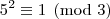
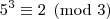
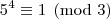
Analogamente, podemos concluir que :
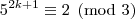
e
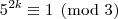
. Assim, como
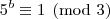
, então

, com
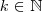
, isto é,

é par!
Como

são ambos pares; sem perda de generalidade diremos que :
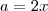
e

, com
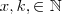
; então:
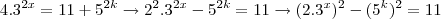
, isto é,
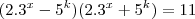
e como

é primo, devemos ter:
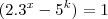
(i)
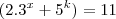
(ii)
já que o primeiro fator é sempre menor que o segundo fator e ambos são naturais devido as condições de contorno do problema.
Somando (i) e (ii) :
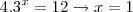
Subtraindo (i) de (ii):
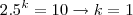
Assim só existe um único valor para

e um único valor para

que satisfazem, simultaneamente, a equação. Concluímos, portanto, que

é a única solução da equação.
Ps. Dava pra encurtar a resolução, mas como o Lorenzo pediu detalhes, achei melhor pormenorizar para ficar mais claro.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aritmética Modular
por Renato_RJ » Dom Fev 20, 2011 19:05
- 5 Respostas
- 2404 Exibições
- Última mensagem por Molina

Ter Fev 22, 2011 10:54
Álgebra Elementar
-
- Aritmética- Duvida em questão do livro praticando aritmética
por wellkirby » Sex Ago 28, 2015 17:37
- 1 Respostas
- 3493 Exibições
- Última mensagem por wellkirby

Seg Set 07, 2015 23:15
Aritmética
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7392 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5630 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2616 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 para a equação
para a equação 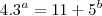
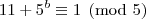 , para todo
, para todo  . Logo
. Logo 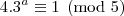 e como
e como  é inversível a
é inversível a 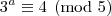
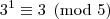
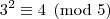
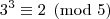
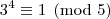
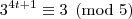
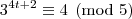
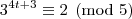
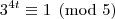
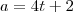 , com
, com 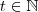 ; que equivale a
; que equivale a 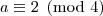 , isto é,
, isto é,  é par!
é par!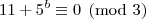 , isto é,
, isto é, 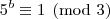
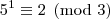
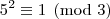
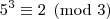
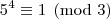
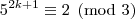 e
e 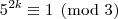 . Assim, como
. Assim, como  , com
, com 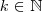 , isto é,
, isto é,  são ambos pares; sem perda de generalidade diremos que :
são ambos pares; sem perda de generalidade diremos que : 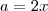 e
e 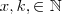 ; então:
; então: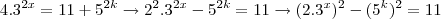 , isto é,
, isto é, 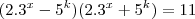 e como
e como  é primo, devemos ter:
é primo, devemos ter: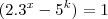 (i)
(i)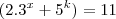 (ii)
(ii)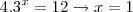
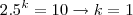
 é a única solução da equação.
é a única solução da equação.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.